As a follow up to a previous question on period finding and factoring, could anyone give a real construction of a 4-qubit circuit that can output (in the same 4-qubit binary format)
$$ a^j \mod{15}$$
for any free choice of $a$ and $j = \{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14\}$, please?
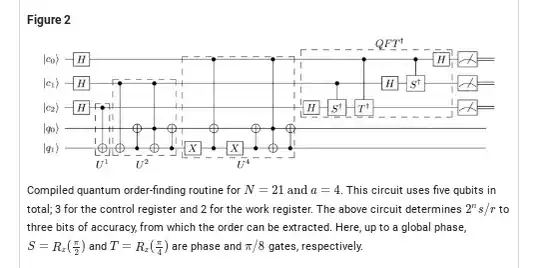
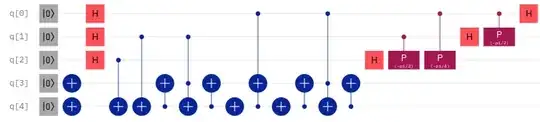
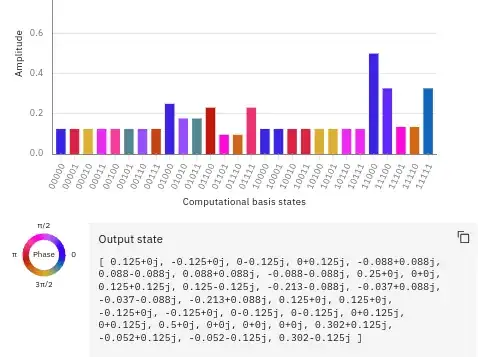
When implementing the Circuit for Shor’s algorithm using 2n+3 qubits I had to use a function like this. You can check out my full implementation of this algorithm here.
You can construct this by first defining a gate that performs addition as follows:
def adder(n, val_a, dag=False):
"""
Construct gate to add val_a into register b in the Fourier basis.
Register b must contain the number on the Fourier basis already.
The subtracter gate gives us b - a if b ≥ a or 2^{n+1}−(a−b) if b < a.
The subtracter is obtained by inversing the adder.
Parameters:
-----------
n: QuantumRegister
Size of register b
val_a: int
Value to which register a will be initialized
dag: Boolean
If set to true, the dagger of the adder gate (the subtracter) is appended
Returns:
--------
adder_gate: Gate
Constructed gate
"""
bin_a = "{0:b}".format(val_a).zfill(n)
phase = lambda lam: np.array([[1, 0], [0, np.exp(1j * lam)]])
identity = np.array([[1, 0], [0, 1]])
arr_gates = []
for i in range(n):
qubit_gate = identity
for j in range(i, n):
if bin_a[j] == '1':
qubit_gate = phase(np.pi / (2 ** (j - i))) @ qubit_gate
arr_gates.append(qubit_gate)
unitary = arr_gates[0]
for i in range(1, len(arr_gates)):
unitary = np.kron(arr_gates[i], unitary)
adder_gate = UnitaryGate(unitary)
adder_gate.label = f"Add {val_a}"
if dag == True:
adder_gate = adder_gate.inverse()
adder_gate.label = f"Subtract {val_a}"
return adder_gate
With this, you can construct a gate that computes $(a + b) \mod N$. So for your case just set $b = 0$ and define $a := a^j$ as you wish. This gate can be defined as follows:
def mod_adder(n, val_a, val_N):
"""
Construct gate to compute a + b mod N in the Fourier basis.
Register b must contain the number on the Fourier basis already.
The answer will be in this register.
Parameters:
-----------
n: QuantumRegister
Size of register b
val_a: int
Value to add to register
val_N: int
We take mod of a + b respect to this value
Returns:
--------
mod_adder_gate: Gate
Constructed gate
"""
reg_c = QuantumRegister(2)
reg_b = QuantumRegister(n)
aux = QuantumRegister(1)
gate = QuantumCircuit(reg_c, reg_b, aux)
qft = QFT(n, name="<span class="math-container">$QFT$</span>").to_gate()
qft_inv = QFT(n, inverse=True, name="<span class="math-container">$QFT^\dag$</span>").to_gate()
gate.append(adder(n, val_a).control(2), reg_c[:] + reg_b[:])
gate.append(adder(n, val_N, dag=True), reg_b[:])
gate.append(qft_inv, reg_b[:])
gate.cx(reg_b[-1], aux[0])
gate.append(qft, reg_b[:])
gate.append(adder(n, val_N).control(1), aux[:] + reg_b[:])
gate.append(adder(n, val_a, dag=True).control(2), reg_c[:] + reg_b[:])
gate.append(qft_inv, reg_b[:])
gate.x(reg_b[-1])
gate.cx(reg_b[-1], aux[0])
gate.x(reg_b[-1])
gate.append(qft, reg_b[:])
gate.append(adder(n, val_a).control(2), reg_c[:] + reg_b[:])
mod_adder_gate = gate.to_gate(label=f"Add {val_a} mod {val_N}")
return mod_adder_gate
For more details on this, you can read the notebook I linked.
There seems no simple general-purpose circuit that can output
$$ a^j \mod{N}$$
for arbitrarily free choice of $a, j, N$.
For instance,
(from https://www.nature.com/articles/s41598-021-95973-w)
uses a very specific circuit that outputs a hard-coded
$$ 4^j \mod{21}$$
while already pre-knowing that the period is 3; thus it is pre-known that a 2 qubit modulo-container register is enough to handle the output period of:
$$4^0 = 1 \mod{21}$$ $$4^1 = 4 \mod{21}$$ $$4^2 = 16 \mod{21}$$ $$4^3 = 1 \mod{21}$$
The three residues are further encoded into 2-bit modulo containers as
$$ 1 \mod{21} \rightarrow |11\rangle$$ $$ 4 \mod{21} \rightarrow |10\rangle$$ $$ 16 \mod{21} \rightarrow |01\rangle$$
only approximately correctly as a waveform:
The final probability spike is not completely clean either:
Thus, the main difficulty in factoring seems to be in implementing an all-purpose circuit for outputing
$$a^j \mod{N}$$
rather than the Fourier transform, which is composed of just $H, P(\theta)$, or the phase estimation.