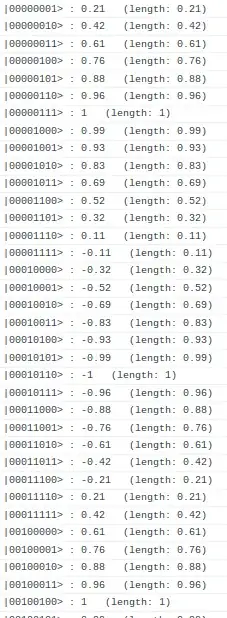
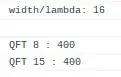
After working through the math, I found that the 3-qubit QFT density transformation is given by the matrix:

(from here)
Extending to $2^8 = 256$ states,



gives the correct single Fourier spike at the right frequency index.
Therefore the error is likely in circuit construction or density state change implementation.
Algebraic verification for 2 qubit QFT circuit:

Step 0:
$$\sqrt{\frac{1}{4}}[a|00\rangle + b|01\rangle + c|10\rangle + d|11\rangle]$$
Step 1:
$$\sqrt{\frac{1}{8}}[(a+c)|00\rangle + (b+d)|01\rangle + (a-c)|10\rangle + (b-d)|11\rangle]$$
Step 2:
$$\sqrt{\frac{1}{8}}[(a+c)|00\rangle + (b+d)|01\rangle + (a-c)|10\rangle + i(b-d)|11\rangle]$$
Step 3:
$$\sqrt{\frac{1}{16}}[(a+b+c+d)|00\rangle + (a-b+c-d)|01\rangle + (a+ib-c-id)|10\rangle + (a-ib-c+id)|11\rangle]$$
$$=\sqrt{\frac{1}{16}}\begin{bmatrix}a+b+c+d \\ a-b+c-d \\ a+ib-c-id \\ a-ib-c+id \end{bmatrix}$$
Comparing with 2 qubit QFT matrix with $\omega = e^{i\frac{2\pi}{4}}$:
$$\sqrt{\frac{1}{4}}\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & \omega & \omega^2 & \omega^3 \\ 1 & \omega^2 & \omega^4 & \omega^6 \\ 1 & \omega^3 & \omega^6 & \omega^9 \end{bmatrix} = \sqrt{\frac{1}{4}} \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i\end{bmatrix}\begin{bmatrix}a\\b\\c\\d\end{bmatrix}=\sqrt{\frac{1}{4}}\begin{bmatrix}a+b+c+d\\a+ib-c-id\\a-b+c-d\\a-ib-c+id\end{bmatrix}$$
The $|01\rangle, |10\rangle$ coefficient entries are reversed, which need to be post-processed.
Algebraic verification of 3 qubit QFT circuit:

$$\boxed{\omega^1 = \frac{1+i}{\sqrt2} \\ \omega^2 = i \\ \omega^3 = \frac{i(1+i)}{\sqrt2} \\ \omega^4 = -1 \\ \omega^5 = -\frac{1+i}{\sqrt2} \\ \omega^6 = -i \\ \omega^7 = -\frac{i(1+i)}{\sqrt3} \\ \omega^8 = 1}$$
Step 0:
$$ \begin{bmatrix} 000 & a \\ 001 & b \\ 010 & c \\ 011 & d \\ 100 & e \\ 101& f \\ 110 & g \\ 111 & h \end{bmatrix}$$
Step 1:
$$ \begin{bmatrix} 000 & a+e \\ 001 & b+f \\ 010 & c+g \\ 011 & d+h \\ 100 & a-e \\ 101& b-f \\ 110 & c-g \\ 111 & d-h \end{bmatrix}$$
Step 2:
$$ \begin{bmatrix} 000 & a+e \\ 001 & b+f \\ 010 & c+g \\ 011 & d+h \\ 100 & a-e \\ 101& w^1b-w^1f \\ 110 & c-g \\ 111 & w^1d-w^1h \end{bmatrix}=\begin{bmatrix} 000 & a+e \\ 001 & b+f \\ 010 & c+g \\ 011 & d+h \\ 100 & a+w^4e \\ 101& w^1b+w^5f \\ 110 & c+w^4g \\ 111 & w^1d+w^5h \end{bmatrix}$$
Step 3:
$$ \begin{bmatrix} 000 & a+e \\ 001 & b+f \\ 010 & c+g \\ 011 & d+h \\ 100 & a+w^4e \\ 101& w^1b+w^5f \\ 110 & w^2c+w^2w^4g \\ 111 & w^2w^1d+w^2w^5h \end{bmatrix}=\begin{bmatrix} 000 & a+e \\ 001 & b+f \\ 010 & c+g \\ 011 & d+h \\ 100 & a+w^4e \\ 101& w^1b+w^5f \\ 110 & w^2c+w^6g \\ 111 & w^3d+w^7h \end{bmatrix}$$
Step 4:
$$ \begin{bmatrix} 000 & a+e + c+g \\ 001 & b+f +d+h \\ 010 & a+e -(c+g) \\ 011 & b+f -(d+h)\\ 100 & a+w^4e+w^2c+w^6g \\ 101& w^1b+w^5f + w^3d+w^7h\\ 110 & a+w^4e -(w^2c+w^6g) \\ 111 & w^1b+w^5f -(w^3d+w^7h) \end{bmatrix}=\begin{bmatrix} 000 & a+e + c+g \\ 001 & b+f +d+h \\ 010 & a+e +w^4c+w^4g \\ 011 & b+f +w^4d+w^4h\\ 100 & a+w^4e+w^2c+w^6g \\ 101& w^1b+w^5f + w^3d+w^7h\\ 110 & a+w^4e +w^6c+w^2g \\ 111 & w^1b+w^5f +w^7d+w^3h \end{bmatrix}$$
Step 5:
$$\begin{bmatrix} 000 & a+c+e+g \\ 001 & b+d+f+h \\ 010 & a+w^4c+e + w^4g \\ 011 & w^2b+w^6d+w^2f+w^6h \\ 100 & a +w^4 e + w^2c +w^6g \\ 101& w^1b +w^5f + w^3d +w^7h \\ 110 & a +w^4 e +w^6c + w^2g \\ 111 & w^3b +w^7f +w^1d + w^5h \end{bmatrix}$$
Step 6:
$$\begin{bmatrix} 000 & a+c+e+g + b+d+f+h \\ 001 & a+c+e+g -(b+d+f+h)\\ 010 & a+w^4c+e + w^4g + w^2b+w^2w^4d+w^2f+w^2w^4h \\ 011 & a+w^4c+e + w^4g - (w^2b+w^2w^4d+w^2f+w^2w^4h) \\ 100 & a +w^4 e + w^2c +w^6g + w^1b +w^5f + w^3d +w^7h \\ 101& a +w^4 e + w^2c +w^6g - (w^1b +w^5f + w^3d +w^7h) \\ 110 & a +w^4 e +w^6c + w^2g + w^3b +w^7f +w^1d + w^5h\\ 111 & a +w^4 e +w^6c + w^2g - (w^3b +w^7f +w^1d + w^5h) \end{bmatrix}$$
$$=\begin{bmatrix} 000 & a+c+e+g + b+d+f+h \\ 001 & a+c+e+g +w^4b+w^4d+w^4f+w^4h\\ 010 & a+w^4c+e + w^4g + w^2b+w^6d+w^2f+w^6h \\ 011 & a+w^4c+e + w^4g + w^6b+w^2d+w^6f+w^2h \\ 100 & a +w^4 e + w^2c +w^6g + w^1b +w^5f + w^3d +w^7h \\ 101& a +w^4 e + w^2c +w^6g + w^5b +w^1f + w^7d +w^3h \\ 110 & a +w^4 e +w^6c + w^2g + w^3b +w^7f +w^1d + w^5h\\ 111 & a +w^4 e +w^6c + w^2g + w^7b +w^3f +w^5d + w^1h \end{bmatrix}$$
$$=\begin{bmatrix} 000&1&1&1&... \\ 001&1&w^4&w^{2\times 4}&... \\ 010&1&w^2&w^{2\times 2}&...\\011&1&w^6&w^{2\times 6}&...\\100&1&w^1&w^{2\times 1}&...\\101&1&w^5&w^{2\times 5}&...\\110&1&w^3&w^{2\times 3}&...\\111&1&w^7&w^{2\times 7}&...\end{bmatrix}\begin{bmatrix}a\\b\\c\\d\\e\\f\\g\\h\end{bmatrix}$$
Renaming labels $q_1 \leftrightarrow q_3$ may be done in post-processing.