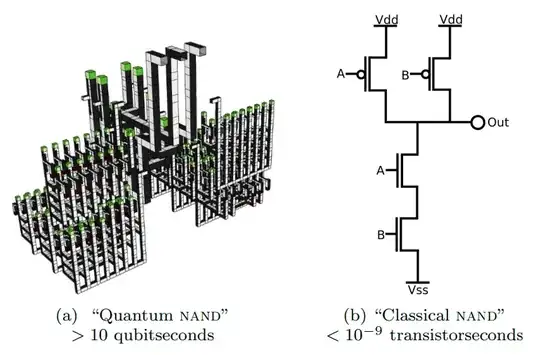
A classical computer takes less than a nanosecond to increment a 64 bit integer.
A superconducting quantum computer takes 10-100 nanoseconds to perform a CNOT gate, the reversible equivalent of a XOR gate. It takes hundreds of CNOT gates, and other gates, to perform a 64 qubit increment. And the result will be quite noisy, because the gates have error rates of around 0.1%.
In my paper on factoring, performing a fault tolerant addition under superposition on 2000-qubit registers is estimated to take around 20 milliseconds. That's roughly the time it takes a typical video game to render a whole frame. For 1 addition. On a building sized machine.
So, no, quantum computers are not faster at incrementing. They are in fact thousands of times to billions of times slower at incrementing. They get their advantage by doing fewer operations, not by doing the individual operations faster.