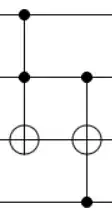
Question
The number of permutation gates on $n$ qubits is $2^n!$. Define an equivalence relation on these gates by $p_1 \approx p_2$ iff $p_1 = C_L p_2 C_R$ where $p_1, p_2$ are $n$-qubit permutation gates and $C_L, C_R$ denote $n$-qubit Clifford gates. What is the number of equivalence classes (defined by this relation) as a function of the number of qubits? We will denote this function by $\mathcal{P}(n)$.Background
From the discussion here What are the relations between the permutation group and the Clifford group?, it is clear that all Clifford permutations are affine permutations. I believe a permutation gate is affine iff it can be expressed as a Clifford permutation. If this is true we can put an upper bound on the number of equivalence classes by using results from the mathematics literature see, for example, chapter 4 here. The number of affine equivalence classes is given there by $1, 1, 4, 302$ for 1,2,3, and 4 bits, respectively. The number of such classes explodes for more bits, but an algorithm is provided to calculate the number for any $n$. I haven't looked closely at this, but it likely intractable to carry out this algorithm for modest $n$.
This number may be only an upper bound on $\mathcal{P}(n)$ since permutations can be equivalent by Hadamard conjugation.
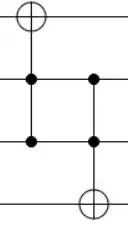
is in the same equivalence class as 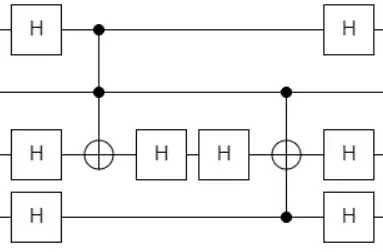
which equals
Are these permutations affine equivalent as well? If so does $\mathcal{P}(n)$ always reduce to counting affine equivalence classes? An affirmative proof of this would answer my question. Otherwise, the question becomes more interesting.