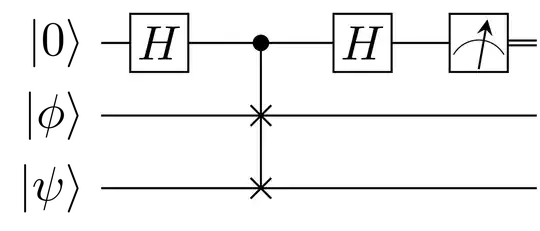
I have seen some sources use a quantum algorithm to estimate inner products between two states. The algorithm used from this answer is shown here:
But this algorithm has limitations; if the inner product is small (less than $\frac{1}{3}$), then the probability of measuring 1 is too low. This can be an issue for vectors that are not orthogonal, but can’t be tested otherwise in a polynomial number of steps.
Is there another quantum algorithm to determine the correct inner product, maybe similar to methods used in QPE, that solve for $N$ times the inner product in binary?
Or is there an algorithm that just tests if two states are orthogonal with accuracy greater than $\frac{2}{3}$?
And of course, we can also introduce an error term in the complexity.