How to determine an unknown quantum gate if we know all other gates in the circuit and the inputs and outputs?

Question

Suppose we have a quantum circuit like this. All the gates are known except for one. For any input of q[0] and q[1], we know the corresponding output. I have provided the output state for four different input state which forms a basis . How can we know that which gate is the unknown gate? 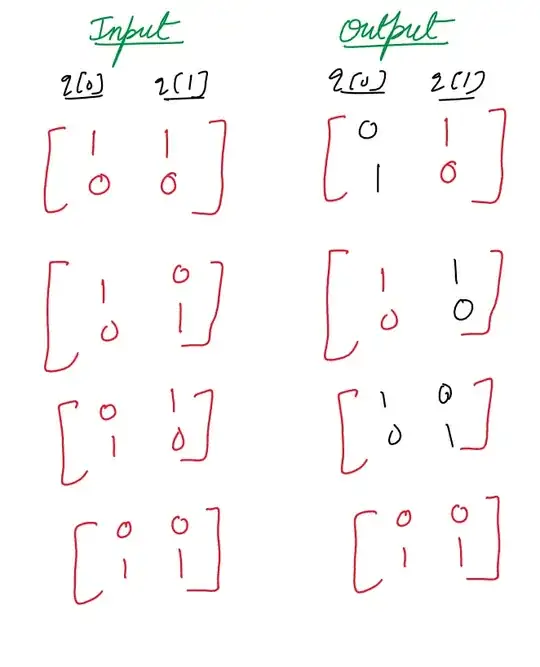How to solve these types of problems?

Answer 1

The effect of a circuit can be explained by matrix-vector multiplications.

If you start with a state $\vec{q}$ and if the gates in your figure are represented by the matrices $A$, $B$, and $U$ (where $U$ is the unknown), then the output will be given by $\vec{q_f} = ABU\vec{q}$.

The $AB$ factor can be replaced by a single matrix called $C$, and with symbolic computation (a.k.a computer algebra) you can combine $U$ and $C$ too.

Let's try this, assuming that your "controlled note" get is just what others usually call "controlled not" or CNOT. Then we have:

$$ A = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix},\tag{1} $$

$$ B = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix},\tag{2} $$

$$ U = \begin{bmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{bmatrix},\tag{3} $$

$$ \vec{q} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix},\tag{4} $$

and

$$ \vec{q}_f = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}.\tag{5} $$

This would mean that we have:

$$\tag{6} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{bmatrix}\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, $$ $$\tag{7} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{bmatrix}\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, $$

$$ \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} f \\ b \\ j \\ n \end{bmatrix}.\tag{8} $$

You now have found 4 out of 16 unknown variables. You can do the same for the other 3 scenarios to get the other 4x3 = 12 unkown variables. You can use this matrix-vector multplier to make the computations easier.