I need the unitary matrix for a full adder. I want to assess how an automatically generated circuit is close to the full adder. Therefore,I need a unitary matrix for the full adder. I believe it should be $2^5 \times 2^5$ (two inputs, two outputs and one carry out). Does anyone have this unitary matrix for the full adder?
-
Welcome to QCSE. Your question seems similar to this one. Or are you asking more about converting an arbitrary truth table specifically into a unitary matrix? – Mark Spinelli Jan 04 '23 at 23:45
-
1Also, please try to avoid postings that use phrases like "I need", as it sounds demanding of volunteers' time. I recommend you edit your posting by clicking on the button next to "Share", to remove the words "I need", and replace them with "I would like". Thanks! – Mark Spinelli Jan 04 '23 at 23:47
2 Answers
A quantum circuit for the full adder is illustrated here:
https://www.quantum-inspire.com/kbase/full-adder/
I think you can easily compute the corresponding unitary matrix.
A study on the implementation of adders is reported in the following recent article:
https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9655478
- 1,554
- 7
- 11
-
thanks, but i font know hot to get the unitary matrix from this circuit. is there any python code? – AMZ Jan 04 '23 at 12:14
A full adder is usually depicted like this, with 1-bit inputs, sum, and carry:
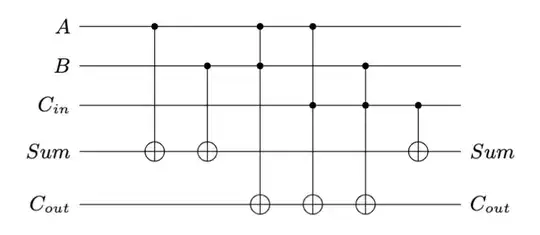
A simple quantum circuit for the corresponding truth table could be drawn like this:
In my own code base, this translates into this code:
psi = ops.Cnot(0, 3)(psi, 0)
psi = ops.Cnot(1, 3)(psi, 1)
psi = ops.ControlledU(0, 1, ops.Cnot(1, 4))(psi, 0)
psi = ops.ControlledU(0, 2, ops.Cnot(2, 4))(psi, 0)
psi = ops.ControlledU(1, 2, ops.Cnot(2, 4))(psi, 1)
psi = ops.Cnot(2, 3)(psi, 2)
return psi
This code applies the gates one after the other. So in order to obtain a single big matrix you have to multiply all the gates together in reverse order and properly pad them to 5 qubits, as in the following (assuming I didn't make a mistake here), where * denotes the Kronecker product and @ is matrix multiply:
M = ((ops.Identity(2) * ops.Cnot(2, 3) * ops.Identity(1)) @
(ops.Identity(1) * ops.ControlledU(1, 2, ops.Cnot(2, 4))) @
(ops.ControlledU(0, 2, ops.Cnot(2, 4))) @
(ops.ControlledU(0, 1, ops.Cnot(1, 4))) @
(ops.Identity(1) * ops.Cnot(1, 3) * ops.Identity(1)) @
(ops.Cnot(0, 3) * ops.Identity(1)) )
The resulting matrix is $2^5 \times 2^5$ and looks something like:
Operator for 5-qubit state space. Tensor:
[[1.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
[0.+0.j 1.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
[0.+0.j 0.+0.j 1.+0.j ... 0.+0.j 0.+0.j 0.+0.j]
...
[0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 1.+0.j 0.+0.j]
[0.+0.j 0.+0.j 0.+0.j ... 1.+0.j 0.+0.j 0.+0.j]
[0.+0.j 0.+0.j 0.+0.j ... 0.+0.j 0.+0.j 0.+0.j]]
This should be relatively simple to achieve in other infrastructures, such as Qiskit. Hope this helps.
- 1,554
- 7
- 11
- 988
- 4
- 12