How to translate a 4-qubit Grover's algorithm circuit into a state Matrix?

Question

Grover's algorithm circuit may be implemented as follows:

(from here)

It is shown very elegantly by @MartinVesely (How to interpret a 4 qubit quantum circuit as a matrix?) how to translate a 4 qubit circuit into its complete matrix representation.

Building on the previous question, I would like translate the full Grover's ciruit into a single state matrix. I attempted as follows:

Op 1: $H \otimes H \otimes H \otimes H$

Op 2: $X \otimes X \otimes X \otimes X$

Op 3: ?

Op 4: $CNOT \otimes I \otimes I$

Op 5: ?

...

Does anyone know how to correctly translate operation 3 and operation 5 in particular into its state matrix, please?

Answer 1

What you have looks like a controlled-U1 gate, which for two qubits has the form:

$$\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i \theta} \end{bmatrix}$$ Notice that the cu1 gate doesn't distinguish between the control qubit and the target qubit. Both give the same result.

The matrix for a cu1 embedded into multiple qubits is a more complicated diagonal matrix, with several of the diagonal entries having the values $e^{i \theta}$

You can use

qc = QuantumCircuit(4)
qc.cu1(.79, 1, 3)
array_to_latex(Operator(qc).data, max_size=100)

to see one example.

Answer 2

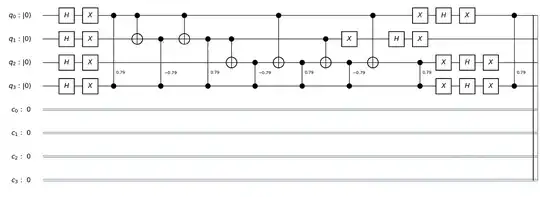
You can figure out 3) and 5) using the formula given by @MartinVesely in the page you linked to.

As was discussed in the post or the matrix of a CU gate with a control and a target separated by $k$ qubits is as follows.

\begin{equation} CU_k = \begin{pmatrix} I_\frac{N}{2}& O_\frac{N}{2} \\ O_\frac{N}{2} &I_\frac{N}{4} \otimes U \end{pmatrix} \end{equation}

Here $N=2^{k+2}$, $O$ is the all-zero matrix and $I$ is the identity. The gates in your diagram seem to be Controlled U1 gates where U1 is represented by the following unitary.

\begin{equation} U1(\lambda) = \begin{pmatrix} 1& 0 \\ 0 &e^{i \lambda} \end{pmatrix} \end{equation}

Now we see there are two qubits between the control and the target qubit of the CU1 gate. Therefore $k=2$ and $N=16$). Substituting in $N=16$ and $U=U1$ we get the following... \begin{equation} CU1_{k=2} = \begin{pmatrix} I_8& O_8 \\ O_8 &I_4 \otimes U1 \end{pmatrix} \end{equation}.

If you have the patience you can write down the full $16 \times 16$ matrix from this by expanding the four entries. Maybe you could factorise this matrix into a tensor product of $2 \times 2$ matrices. I'd have to think about it more as I'm not sure there is a nice form.

Edit: Similarly to Frank I calculated the unitary (I did the first CU1 gate in the circuit). Wouldn't want to do this by hand.

I did this symbolically with pytket. Note the factor of $\pi$ due to different conventions. $(\lambda = \pi \theta)$

from pytket import Circuit, OpType
from pytket.utils import circuit_to_symbolic_unitary
from sympy import Symbol
theta = Symbol("theta") #theta = 1 / 4 in your example
circ = Circuit(4).add_gate(OpType.CU1, [theta], [0, 3])
circuit_to_symbolic_unitary(circ)