Today's Quanta Magazine article says "But it’s proved difficult to find examples of any algorithms with a clear “quantum advantage” that enables performance beyond the reach of classical machines."
Does factoring integers to break public key cryptography still have an advantage on quantum computers? What about solving NP-complete problems like SAT? Anything else?
"But it’s proved difficult to find examples of any algorithms with a clear “quantum advantage” that enables performance beyond the reach of classical machines."
The author is commenting on the fact that quantum computers have not solved any real-world problem faster than a classical computer can, even though we know that the number of quantum operations necessary to, for example factor integers, scales more slowly with the size of the problem as the number of classical operations would.
Even though this statement was not written by an expert in the field (it was written by someone who describes herself as a "writing intern" at Quanta Magazine), I agree 100% with her statement. It is true that quantum computers (even the one in Google's "quantum supremacy" experiment) have only been able to do some simple tasks that don't compute anything useful in terms of the purpose of computers.
This doesn't rule out the possibility that some breakthrough in the future might make quantum computing have more clear advantages over classical computing.
"Does factoring primes to break public key cryptography still have an advantage on quantum computers?
There's more than one thing to say here. Number one is that "factoring numbers" isn't enough to "break public key cryptography". It's basically enough to break RSA public key cryptography, but people have already started moving away from RSA. For example my SSH keys to push commits to GitLab use an algorithm based on twisted Edwards curves which is recommended more strongly by GitLab than RSA.
The second thing I'll say is that even if being able to factor large integers were to be enough for breaking all public key cryptosystems (it's not!), you're right that classical computers currently have the practical advantage here. Classical computers have factored huge numbers like RSA-230, whereas quantum devices would probably need millions if not billions of qubits to factor a number of that size. Even Google and IBM do not pretend to have quantum computers with a thousand qubits, let alone the millions or billions of qubits that would be needed in order to have an advantage over classical computers for factoring.
"What about solving NP-complete problems like SAT? Anything else?"
This diagram (from here) shows that the QMA complexity class does possibly have some overlap with the class of NP-hard problems, but is not expected to be able to cover all NP-hard problems:
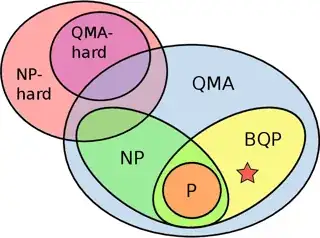
Therefore, some NP-hard problems may be even too difficult for a perfectly operational quantum computer to solve efficiently!
