My First Own Grover Search with Q#

Question

After I read the "[Quantum computing foundations](https://learn.microsoft.com/en-us/training/paths/quantum-computing-fundamentals/) of Microsoft I would like to be sure I understand a little the things. So, I code my own Groover search. The problem is simple. My code wants retrieve the index in array given a value. The very simple example is I have an array ["A", "B", "C", "D"] and the given value is "B" so I would like have as result 1.

I have 2 errors for the moment:
First, I have an error with my function to retrieve the index, but I think it's a little thing.

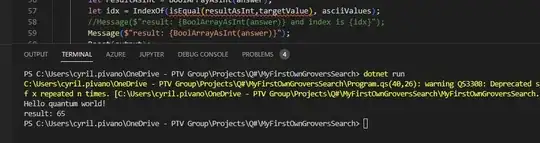
Secondly (and most important), the output register returns me an array of bits matching with "A" and not "B" as I wish.

Someone could help me understand what I am doing wrong.

namespace MyFirstOwnGroversSearch {
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Diagnostics;
open Microsoft.Quantum.Arrays;
open Microsoft.Quantum.Math;
open Microsoft.Quantum.Measurement;



@EntryPoint()
operation MyFirstOwnGroverSearch() : Unit {
    Message("Hello quantum world!");
    let values = ["A","B","C","D"];
    let asciiValues = [65,66,67,68];
    let asciiValuesAsBooleans = [IntAsBoolArray(65,7), IntAsBoolArray(66,7), IntAsBoolArray(67,7), IntAsBoolArray(68,7)];

    use (registerToBeMatched) = (Qubit[7]);
    // prepare registerToBeMatched -> apply an X gate to each qubit that corresponds to "true" bit in the bit string.
    let targetValue = 66; // "B";
    let targetValueAsBool = IntAsBoolArray(targetValue,7); 
    ApplyPauliFromBitString(PauliX, true, asciiValuesAsBooleans[0], registerToBeMatched);

    use target = Qubit();

    let markingOracle = MarkEquality(_,_,_); // put target to 1 if arrays bits are equals ( first and second args)
    let phaseOracle = ApplyMarkingOracleAsPhaseOracle(markingOracle,_,registerToBeMatched);

    // Define the parameters of the search.
    // Each character is described using 7 bits (or qubits).
    let nQubits = 7;
    // The search space is all bit strings of length nQubits.
    let searchSpaceSize = 2 ^ (nQubits);
    let nSolutions = 1;
    // The number of iterations can be computed using a formula.
    let nIterations = Round(PI() / 4.0 * Sqrt(IntAsDouble(searchSpaceSize) / IntAsDouble(nSolutions)));

    mutable answer = new Bool[nQubits];
    use (register, output) = (Qubit[nQubits], Qubit());
    mutable isCorrect = false;
    repeat {
        RunGroversSearch(register, phaseOracle, nIterations);
        let res = MultiM(register);
        // Check whether the result is correct.
        markingOracle(register, registerToBeMatched, output);
        if (MResetZ(output) == One) {
            set isCorrect = true;
            set answer = ResultArrayAsBoolArray(res);
        }
        ResetAll(register);
    } until (isCorrect);

    // Convert the answer to readable format (actual graph coloring).
    let resultAsInt = BoolArrayAsInt(answer);
    let idx = IndexOf(isEqual(resultAsInt,targetValue), asciiValues);
    //Message(<span class="math-container">$"result: {BoolArrayAsInt(answer)} and index is {idx}");
Message($</span>&quot;result: {BoolArrayAsInt(answer)}&quot;);
    Reset(output);
    ResetAll(registerToBeMatched);
}

operation isEqual (a: Int, b: Int) :  Bool {
    return (a == b);
}

operation MarkEquality(c0 : Qubit[], c1 : Qubit[], target : Qubit) : Unit is Adj+Ctl {
    within {
        for (q0, q1) in Zipped(c0, c1) {
            // Compute XOR of bits q0 and q1 in place (storing it in q1).
            CNOT(q0, q1);
        }
    } apply {
        // If all computed XORs are 0, the bit strings are equal - flip the state of the target.
        (ControlledOnInt(0, X))(c1, target);
    }
}    

operation ApplyMarkingOracleAsPhaseOracle(
    markingOracle : ((Qubit[], Qubit[], Qubit) =&gt; Unit is Adj), 
    c0 : Qubit[],
    c1 : Qubit[]
) : Unit is Adj {
    use target = Qubit();
    within {
        // Put the target qubit into the |-⟩ state.
        X(target);
        H(target);
    } apply {
        // Apply the marking oracle; since the target is in the |-⟩ state,
        // flipping the target if the register state satisfies the condition 
        // will apply a -1 relative phase to the register state.
        markingOracle(c0, c1, target);
    }
}

operation RunGroversSearch(register : Qubit[], phaseOracle : ((Qubit[]) =&gt; Unit is Adj), iterations : Int) : Unit {
    ApplyToEach(H, register);

    for _ in 1 .. iterations {
        phaseOracle(register);
        within {
            ApplyToEachA(H, register);
            ApplyToEachA(X, register);
        } apply {
            Controlled Z(Most(register), Tail(register));
        }
    }
}


}
```