I have a question about how to transform a quantum gate into the matrix representation. For example, we all know the 2-qubit gate--CNOT, can be written like
\begin{pmatrix}
1& 0& 0& 0 \\
0& 1& 0& 0 \\
0& 0& 0& 1 \\
0& 0& 1& 0 \\
\end{pmatrix}
and its image is shown on the lefe side of the following picture:
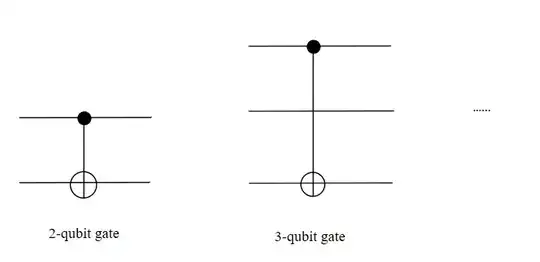
However, I don't konw how to transform the 3-qubit gate into matrix representation. It doesn't look like to directly utilize tensor product technique, and therefore I want to know how to transform them? Probabily in $C_1T_3Q_3$ or in $C_2T_5Q_6$ these more general situation, where $C_k$ stands for the k-th control qubit, $Q_j$ stands for the j-th target qubit, and $Q_i$ means that there are i qubits in total.