I was solving Controlled H gate from qiskit textbook -> Basic Circuit Identities
There I tried to find the unitary matrix for CH gate but it get's really complicated when I use tensor product or other stuff. Is there any shortcut to prove that the given circuit is the equivalent to CH gate --- Circuit is -->
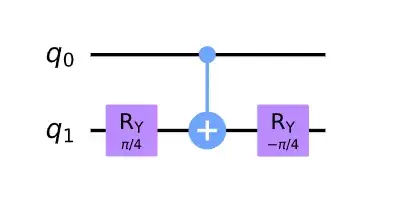
The shortcut is to think about what happens to $q_1$ in the two separate cases of $q_0$ being either $|0\rangle$ or $|1\rangle$. If it works for both of those, then by linearity it works on all inputs.
So, if $q_0$ is in $|0\rangle$, the controlled-not does nothing. Effectively,the only gates that act on $q_1$ are two single-qubit gates which are the inverse of each other. Hence, the net effect is the identity.
If $q_0$ is in $|1\rangle$, the controlled-not applies $X$ on $q_1$. Hence, the net sequence is $$ R_Y(-\pi/4)XR_Y(\pi/4). $$ You could just multiply this out. Alternatively, use commutation relations: $$ R_Y(\theta)X=XR_Y(-\theta). $$ Thus, the net gate is $$ XR_Y(\pi/2)=X(I-iY)/\sqrt{2}=(X+Z)/\sqrt{2}. $$
Your overall description is "if $q_0$ is in 0, do nothing, otherwise apply Hadamard". In other words, controlled-Hadamard.
