4

First, I would like to state that I went through many excellent sources of information (among them - Grover's original paper, several QCSE posts like 1 2, and many more sources) - And yet I couldn't find a satisfying answer, so there must be something I don't understand.

I am trying to settle my mind with the known fact that Grover's algorithm can retrieve a specific value $w$ from an unsorted list in $O(\sqrt{N})$ steps, while $N$ is the size of the list. It is understood that $\frac{\pi}{4}\sqrt{N}$ iterations over Grover's iterator (Grover's oracle + diffuser operator) are needed, which may implies upon an overall computational complexity of $O(\sqrt{N})$.

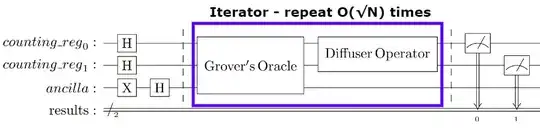enter image description here Grover's algorithm with n = 2, N = 4, one iteration over Grover's iterator.

But since Grover's orcale + diffuser are nested inside the iterator, as I understand it - We should be able to implement both of them independently of $N$, such that in each iteration both the oracle and the diffuser should contribute $O(1)$ steps to the overall complexity - If we want to achieve an overall complexity of $O(\sqrt{N})$.

There are several ways to implement the oracle and the diffuser, but as far as I understand - a multi-controlled gate over the $n = log(N)$ qubits in the counting register is unavoidable, in both:

Implementation of the diffuser

Implemention of the diffuser for n = 4 qubits with an mcz gate.

Implementation of the oracle

Implemention of the oracle for the $w = 1001$ with an mcx gate.

Decompositon of such multi-controlled gates would produce a circuit depth dependent of $n = log(N)$. So if in each iteration at least $O(log(N))$ steps being performed, then it seems to me that the overall complexity of the algorithm should be at least $O(\sqrt{N} \ log(N))$.

What am I missing? How is the overall complexity of $O(\sqrt{N})$ is being achieved after all?

Thanks!

Ohad
  • 1,739
  • 2
  • 15

1 Answers1

6

The complexity for an oracle-based algorithm (e.g. in the case of search) is only counted in terms of the number of calls to the oracle. Yes, if you tried to implement a given oracle, it could be hugely costly (that's the whole point of the oracle-based counting), and that cost could grow with the system size. But that aspect is not taken into account.

If you want to view it another way, we're counting the number of oracle calls. The oracle has to be made out of a circuit. So, at worst, your running time is (number of calls to oracle)$\times$(circuit size of oracle). BUT, this overhead is true both for the quantum search and the classical search. Since the quantum computer could just implement the classical algorithm, it's going to be no worse (although there's some chance there could be a better quantum algorithm). Thus, the gap between quantum/classical is evident from the number of calls to the oracle.

DaftWullie
  • 57,689
  • 3
  • 46
  • 124
  • @ DaftWullie thanks for the answer. I get the point that the oracle is being called $O(\sqrt{N})$ times insteaf of $N$ calling to $f(x)$ classically. However, what's the good in that if the oracle can't be implemented independently of $N$? I was thinking that by assuming that the oracle acts in one step, there's a a basis of $O(1)$ possible implementation of the oracle. In addition - It also looks that any implementation of the diffuser also depends on $N$, so what's the reasoning for that? Thanks a lot! – Ohad Aug 26 '22 at 03:10
  • I would say that the oracle is always going to be a computation involving all the bits, so it's going to take a time at least $O(n)$ (with n=\log N$). In fact, you'd be pretty amazed if that's all it was. On the other hand, you're solving an NP problem, so you're guaranteed to be able to recognise a solution efficiently. This means your oracle runs in a time polynomial in n. – DaftWullie Aug 26 '22 at 07:02
  • Thus, the running time of an oracle, in practice, is going to be vastly higher than all the gates surrounding it, i.e. the diffuser. So, we don't worry about the cost of the diffuser. But the whole point is that $\sqrt{2^n}\text{poly}(n)$ is so much better than $2^n\text{poly(n)}$ (given that they're the same polynomial). – DaftWullie Aug 26 '22 at 07:02
  • Still don't get it. Let's assume I accept the claim that the oracle is a magical black box, I don't care what's inside and considering it as 1 step. Still, the diffuser is nested inside the iterator, so if we want to claim for $O(\sqrt{N})$ overall complexity for Grover's algorithm, we must prove that we can implement the diffuser in $O(1)$ steps. I am focusing my wonders on the claim that Grover's algorithm achieves a complexity of $O(\sqrt{N})$ - Regardless the comparison to the classical case. – Ohad Aug 27 '22 at 12:30
  • Grover's algorithm only achieves a complexity $O(\sqrt{N})$ with respect to the oracle. It is not a claim that any search protocol takes $O(\sqrt{N})$ steps when you take the full circuit implementation into account. – DaftWullie Aug 30 '22 at 06:49
  • I understand, but - The diffuser is not a part of the oracle. To my understanding implementing the diffuser is dependent of $n = log(N)$, so if we repeat the iterator $O(\sqrt{N})$ times, the overall complexity is at least $O(\sqrt{N}\ log(N))$. I.e there must be a way to implement the diffuser in $O(1)$ steps for an overall complexity of $O(\sqrt{N})$ - But to my understanding that's not possible. – Ohad Aug 30 '22 at 10:41
  • There are two different complexity measures. Either you measure the complexity with respect to an oracle. Then, complexity is simply the count of the number of uses of the oracle, $O(\sqrt N)$. All other gates are considered "for free". Or you measure the circuit complexity of implementing a specific oracle. The oracle requires $O(f(n))$ gates where $f$ is a polynomial in $n$, and the complexity is then $O(\sqrt{N} f(n))$. The diffuser is irrelevant because the $O(n)$ is beaten by the $O(f(n))$. – DaftWullie Aug 30 '22 at 11:13
  • OK, got that, Thanks! Just to conclude - What I infer from our discussion is that Grover's algorithm is more a proof-of-concept rather than a real efficient search algorithm. I.e it allows O$(\sqrt{N})$ calls to an oracle compared to $O(N)$ calls to the same oracle (classically implemented) in the classical case. However, it is possible that going over the entries of the list one-by-one in the simple classical case might be more efficient. – Ohad Aug 30 '22 at 12:26
  • No! Going over a list one by one requires time $O(N f(n))$, which is worse. So there is a massive speed improvement for Grover's search. That said, it is not, and has never claimed to be an efficient search algorithm. That would require a running time that's polynomial in $n$. – DaftWullie Aug 30 '22 at 12:31
  • OK, I think I understand what was the confusion all about. I was thinking that if the value we are seeking to retrieve is $w$, and given an arbitrary input $x$ from the list - It can be verified classically in $O(1)$ steps whether $x = w$ or not. But of course this action classically also depends on the number of bits $n = log(N)$. So indeed Grover's algorithm provides an actual quadratic speedup compared to the classical brute-force algorithm, with respect to an oracle. Your'e right about the inappropriate use of the term efficient, I meant more efficient than the classical case. Thanks! – Ohad Aug 30 '22 at 15:06
  • 1
    Exactly! The key is that both the quantum and classical oracle will have the same dependence on $n$.

    I don't know that technically an "efficient" algorithm has to mean that it's $poly(n)$, I think it's just something that is commonly used. Grover's algorithm is provably the best you can do in terms of an unstructured search (https://arxiv.org/abs/quant-ph/9605034), so in some sense it is actually the most efficient search algorithm you can come up with! On another note, the speed improvement is asymptotic because the constant quantum overheads in reality are brutal

     – sheesymcdeezy Aug 31 '22 at 17:49