1

I am relative beginner to building qc circuits and programming. Please share with me how you would begin to approach this problem. What steps would you take to draw this circuit? Thank you for your help.

What I have worked on thus far:

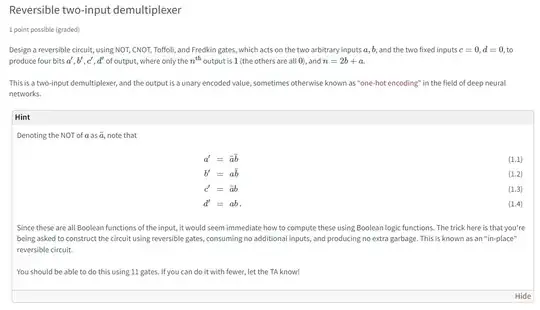
  1. I have studied the basic idea of a demultiplexer. However, I do not know what the selector switch(s) would be in this case so I will assume the NOT, CNOT, Toffoli and Fredkin gates will play this role?

  2. Using the HINT, I was able to construct a table:

a, b, c, d to a(bar)b(bar), ab(bar), a(bar)b, ab [n]

0 0 0 0 1 0 0 0 n= 2b + a = 0

1 0 0 0 0 1 0 0 n= 2b + a = 1

0 1 0 0 0 0 1 0 n= 2b + a = 2

1 1 0 0 0 0 0 1 n= 2b + a = 3

  1. My first question re: "where only the nth output is 1 (the others are all 0 ), and n=2b+a ."

If a and b inputs are arbitrary, how do I ensure the appropriate nth output? If for n=1, a=1 and b=0 (vs. a=0,b=0), what can I do to ensure that for n=1 the output is 1 0 0 0.

  1. Second question, should I be using a circuit composer at this stage? If so, how do I begin to think about arbitrary nature of inputs a and b with respect to the boolean logic gates?

Any guidance and hints are appreciated.

Reversible 2-bit demultiplexer

sivaguru42
  • 11
  • 2
  • 1
    See if you can start by solving this problem as a classical logic circuit, or solving the simpler version where you go from 1 binary bit to 2 unary bits instead of 2-to-4. – Craig Gidney Jul 29 '22 at 17:04

2 Answers2

1

Regarding question 4, for this particular problem, the first useful thing to know is $\text{Toffoli}(a,b,0)$ gives an $\text{AND}$ gate. (I think this question comes from the MIT course, so I'm adopting their notation in the problem set.)

  • So, to have $d'=ab$, we just need a $\text{Toffoli}(a,b,d)$.
  • Similarly, to get $c'=\bar{a}b$, we can do a $\text{Toffoli}(\bar{a},b,c)$.

At this point, we want to get $a'$ and $b'$ without changing the values of $c'$ and $d'$, this means that we need to use some of $a, b$ (or $\bar{a}, \bar{b}$), $\bar{a}b$, and $ab$ to obtain $\bar{a}\bar{b}$ and $a\bar{b}$. I personally tried a little, $\text{Fredkin}$ gate feels irrelevant here, because the Hamming weight does change. As for $\text{Toffoli}$, $c', d'$ should stay unchanged, but the $\text{AND}$ of them, $c'd'$, doesn't make sense. So the second useful observation is $\bar{a} \oplus \bar{a}b = \bar{a}\bar{b}$. (One way to see it is through case analysis.)

  • Then to get $a'$, we can do a $\text{CNOT}(c', \bar{a})$.
  • Finally, to get $b'$, we can similarly use $\text{CNOT}(a', \bar{b})$.
user23479
  • 11
  • 2
0

For your first question:

There are two input bits, so $2^2=4$ possible input. And $n$ takes different values for different inputs as you have worked out. If you make sure the four wires in your circuit give the output as eq. 1.1-1.4 suggested, then the circuit gives the correct result for arbitrary input $a$ & $b$. For example, we know $d = 0$. If we apply the Toffoli gate $\text{toffoli}(a, b, d=0)$ then $d' = ab\oplus d = ab$. The fourth wire in the problem is essentially solved if you don't do anything to it after this gate. But you have to solve the other three now.

For your second question:

I would just take $a$ and $b$ as unknowns. I find it simplifies things if you draw a $2\times2$ matrix. For example, $$a = \begin{pmatrix} 0 & 1 \\0 & 1\end{pmatrix},\ b = \begin{pmatrix} 0 & 0 \\1 & 1\end{pmatrix},\ ab = \begin{pmatrix} 0 & 0 \\0 & 1\end{pmatrix},\ \bar{a}b = \begin{pmatrix} 0 & 0 \\1 & 0\end{pmatrix}\ldots$$ Then I can quickly see if I add ($\oplus$ via CNOT or Toffoli) $b$ to $ab$, I get $\bar{a}b$. Hopefully this can get you started.

I am not sure how the number 11 comes about. I only used 10 gates to get the right answer.

QBarista
  • 1
  • What matrices $a$ and $b$ mean? They are neither gates nor description of quantum states... – Martin Vesely Feb 20 '23 at 09:48
  • @MartinVesely Good point. I am really using the small matrix to keep track of the 4 possible inputs. It helps me to do gate operations on them. For example, a CNOT(a, b) gives $$a\oplus b = \begin{pmatrix} 0 & 1 \ 1 & 0\end{pmatrix},$$ which says if $a=0, b=0$ then CNOT gives 0; if $a=1, b=0$ then CNOT gives 1, etc. I am sure more sophisticated people don't have to do this but this helps me. – QBarista Feb 21 '23 at 17:44