0

Setting

I have a (6 qubit) circuit which implements a unitary $U$.

Goal

I need the circuits which implement $-U, iU, -iU$.

Phase matters, because I later embed a controlled version of $\pm i U $ into a bigger circuit.

Attempt

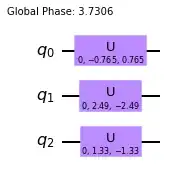
for 3 qubits, Qiskit decomposes e.g. $-i$ into

qnum = 3

unitary = -1j * np.eye(2**qnum)


_qc = QuantumCircuit(qnum)
_qc.unitary(unitary, [*range(qnum)], label='U1')


_qc = transpile(_qc, backend=AerSimulator(), optimization_level=3, basis_gates=['cx', 'id', 'u3'])
_qc.decompose().draw('mpl')

3 qubits, -1j

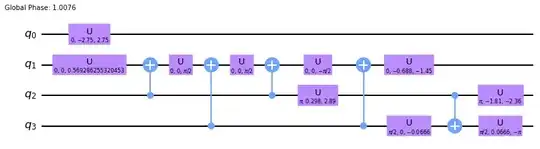
And for four qubits (qnum=4):

4 qubits, -1j

Both decompositions are not obvious to me.

Is it known how to find the right gates analytically?

Is this decomposition for 4 qubits really optimal?

Andreas Burger
  • 301
  • 1
  • 11
  • You almost certainly want to get the "global" phase by applying an appropriate Rz(theta) to the later control, instead of by tweaking the circuit being controlled. This will tend to produce a smaller result, since you'll use a a single Z rotation instead of multiple controlled operations to get the effect you're going for. – Craig Gidney Jun 25 '22 at 17:14
  • You are right, the controlled version of two gates (x, u from Egretta Thula's answer) per qubit quickly becomes a lot. What do you mean by applying 'appropriate Rz(theta) to the later control'? You mean applying Rz to the controlling qubits? How does that work? – Andreas Burger Jun 26 '22 at 03:10

1 Answers1

4

To add a global phase $\phi$, all what you need is to apply $X$-gate followed by $U(\pi, \phi, \phi + \pi)$ to any qubit in your circuit.

For example to implement $iU$, we have $\phi = \frac{\pi}{2}$.

You can use the matrix representation of U-gate to check this. Or, just use the following code to check:

from qiskit import QuantumCircuit
from qiskit.quantum_info.operators import Operator
from qiskit.visualization import array_to_latex
import numpy as np

circ = QuantumCircuit(3)


phase_angle = np.pi / 2


circ.x(0)
circ.u(np.pi, phase_angle, np.pi + phase_angle, 0)


Check:


op = Operator(circ)
array_to_latex(op)

Similarly, you can implement $-U$, and $-iU$ by setting phase_angle to $\pi$, and $\frac{3\pi}{2}$ respectively.

$iU$ circuit should look like:

enter image description here

Egretta.Thula
  • 9,972
  • 1
  • 11
  • 30
  • Do you happen to know, if a circuit has an overall phase, is there a better way to construct its controlled version than just naively controlling the construction you provide here? (for more than a single ancillary qubit) – mavzolej Feb 23 '24 at 22:16