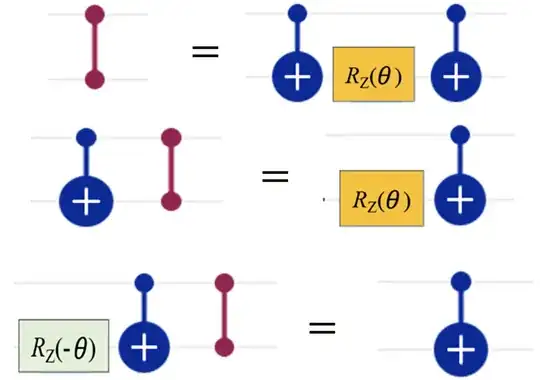
These are indeed correct. See this paper as well starting at Eq. (31).
Start with the first equivalence: ZZ $\equiv$ CNOT$^{(0,1)}$ $R_Z^{(1)}(\theta)$ CNOT$^{(0,1)}$ as given, though you can compute this in terms of exponentiated Pauli operators. From your question, I'm guessing you aren't asking about that though.
To get the 2nd equivalence, we have CNOT$^{(0,1)}$ ZZ $=$ CNOT$^{(0,1)}$ CNOT$^{(0,1)}$ $R_Z^{(1)}(\theta) $ CNOT$^{(0,1)}$. Notice the two CNOT gates next to each other. Those cancel each other out becoming the identity CNOT$^{(0,1)}$ CNOT$^{(0,1)}$ = $\mathbb{1}$. So you get CNOT$^{(0,1)}$ ZZ $\equiv$ $R_Z^{(1)}(\theta) $ CNOT$^{(0,1)}$.
The 3rd equivalence is the same trick but we also cancel the $R_Z$ gate: $R_Z^{(1)}(-\theta)$ CNOT$^{(0,1)}$ ZZ $=$ $R_Z^{(1)}(-\theta)$ CNOT$^{(0,1)}$ CNOT$^{(0,1)}$ $R_Z^{(1)}(\theta) $ CNOT$^{(0,1)}$. We reduce the CNOTs just like before: $R_Z^{(1)}(-\theta)$ CNOT$^{(0,1)}$ ZZ $=$ $R_Z^{(1)}(-\theta)$ $R_Z^{(1)}(\theta)$ CNOT$^{(0,1)}$. Now we have two single qubit gates that also cancel each other out $R_Z^{(1)}(-\theta)$ $R_Z^{(1)}(\theta) = \mathbb{1}$. So we get $R_Z^{(1)}(-\theta)$ CNOT$^{(0,1)}$ ZZ $=$ CNOT$^{(0,1)}$