3

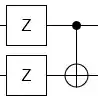
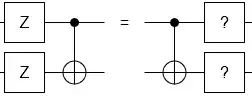
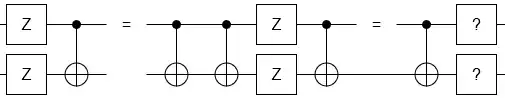
According to Fowler, Mariantoni, Martinis, and Cleland, 2012, Surface codes: Towards practical large-scale quantum computation (PRL link, page 29), braiding transformations are doing the same thing that CNOT and its adjacent are doing to 2Q gates:

$$\hat{CNOT}\:^\dagger\big(\hat I\otimes\hat X\big)\hat{CNOT}\:^=\hat I\otimes \hat X,\\ \hat{CNOT}\:^\dagger\big(\hat X\otimes\hat I\big)\hat{CNOT}\:^=\hat X\otimes \hat X,\\ \hat{CNOT}\:^\dagger\big(\hat I\otimes\hat Z\big)\hat{CNOT}\:^=\hat Z\otimes \hat Z,\text{and}\\ \hat{CNOT}\:^\dagger\big(\hat Z\otimes\hat I\big)\hat{CNOT}\:^=\hat Z\otimes \hat I.$$

which is exactly what a braiding transformation is doing.

And they say that therefore, braiding is analogous to CNOT.

But I say no! - it is analogous to $$\hat{CNOT}\:^\dagger\big(2Qubit Operator)\hat{CNOT}\:^.$$ which is 2 CNOTs, and not one CNOT!

Can someone settle this for me please?

Thank you!

Ron Cohen
  • 1,194
  • 3
  • 17
  • Important detail: It's not $C^\dagger P$ it's $C^\dagger P C$. The Clifford conjugates the pauli product. More relevant to answering: I'm not sure what you think $C$ is. You seem to think it's a number and not a matrix? What do you think the value $C \times C - 2$ is equal to? – Craig Gidney Jan 05 '22 at 16:30
  • @CraigGidney - that was my bad from the original edit to latex. The OP has clarified. Sorry! – Mark Spinelli Jan 06 '22 at 14:12

3 Answers3

2

They are considering the adjoint action of CNOT, i.e. its action as a quantum channel on density matrices, see also this recent question.

Since the Pauli operators form a basis for the vector space of linear operators, it is enough to know the action of a quantum channel on those. Moreover, for unitaries, it is even enough to know it on a set of generators of the Pauli group, like in this case $I\otimes X, X\otimes I, I\otimes Z, Z\otimes I$. This is because we have $$ U PQU^\dagger = UPU^\dagger UQU^\dagger, $$ so the image of $PQ$ is simply the product of the images of $P$ and $Q$.

This is a very common thing to do, especially if you are dealing with Clifford gates.

Hence, braiding effectively gives you the same quantum channel as a CNOT gate. This determines the underlying unitary up to a global phase. But since the latter is anyway not measurable, this is completely fine.

Markus Heinrich
  • 4,882
  • 8
  • 17
  • Thank you. But - I think this is not the answer. It is correct to say that this is in terms of density matrices! so when making transormation, it is not like making a gate. trnasformation is something that has to be done on the right and on the left, so that after multiplying |Psi> in the right and left, it will get the CNOT to both terms. – Ron Cohen Jan 09 '22 at 08:59
  • @RonCohen I do not understand your comment. – Markus Heinrich Jan 10 '22 at 09:35
2

[Paraphrased: Why does $C^\dagger P C$ use $C$ twice? In the circuit it's only there once!]

Consider a Pauli product $P = Z \otimes Z$ before a CNOT $C$ in a quantum circuit:

enter image description here

We want to know what the CNOT transforms this Pauli product into. We want to know what the Pauli product becomes on the right hand side of the CNOT:

enter image description here

Note that it is always the case that $C^\dagger C = I$. In other words, we can insert a pair of CNOTs anywhere into the circuit and not change it:

enter image description here

But, in the middle expression, notice we can now switch our focus from "the original CNOT is the rightmost CNOT" to "the original CNOT is the leftmost CNOT". Meaning the series of operations $CNOT \cdot (Z \otimes Z) \cdot CNOT$ must equal our mystery product. And the reason there's a pair of them is because we inserted a pair of self-cancelling operations to allow ourselves to shift focus.

Another way to understand what is happening is to realize that saying

$$P_{after} = C P_{before} C^\dagger$$

is the same as saying (right multiply by $C$):

$$P_{after} \cdot C = C P_{before} C^\dagger C$$

which is the same as saying (cancel $C^\dagger C = I$)

$$P_{after} \cdot C = C \cdot P_{before}$$

In words: there was a matching mystery for why $P_{after}$ had NO cnots, instead of 1 cnot. It turns out the missing cnot was the extra cnot beside $P_{before}$. The equation was originally telling us how to move the one CNOT from one side of the Pauli product to the other, and then we solved for $P_{after}$ which rearranged things.

Craig Gidney
  • 36,389
  • 1
  • 29
  • 95
  • Thank you. But - I think this is not the answer. It is correct to say that this is in terms of density matrices! so when making transormation, it is not like making a gate. trnasformation is something that has to be done on the right and on the left, so that after multiplying |Psi> in the right and left, it will get the CNOT to both terms – Ron Cohen Jan 09 '22 at 08:59
  • @RonCohen No, this isn't about density matrices. It's about stabilizers. If you know N stabilizer generators that a state is in the +1 eigenstate of, then you know the state. Tracking what those Pauli products turn into as they move through Clifford operations is how you track the state through Clifford operations. That's how (many) stabilizer simulators work. Knowing that the Pauli products do the right thing therefore tells you that the operation is doing the right thing. – Craig Gidney Jan 09 '22 at 18:39
  • @CraigGidney but it's not about tracking a (specific) stabilizer state. It's about confirming that an operation is doing the right thing, on all states. Certainly, it's enough to check it on stabilizer states, but this is not the point. Checking it on a basis would be the sensible thing. – Markus Heinrich Jan 10 '22 at 09:35
  • @MarkusHeinrich A Clifford operation is uniquely defined (up to global phase) by how it conjugates generators of the Pauli group over the qubits it acts on. Try to find a counterexample. If you know it's a Clifford operation and you know it sends Paulis to the right thing, you know it's the right operation. – Craig Gidney Jan 10 '22 at 13:02
  • @CraigGidney Indeed, but this is true for any unitary (see my answer). Cliffords are only special because the images happen to be Pauli operators, too (up to a phase). I guess we mean the same thing. I just wanted to point out that it is indeed important that Pauli operators form a basis, otherwise you wouldn't completely specify the operation. – Markus Heinrich Jan 11 '22 at 09:14
1

A quote in Fowler, Mariantoni, Martinis, and Cleland, 2012, "Surface codes: Towards practical large-scale quantum computation" (page 22) a few pages earlier than my question. I refer to the CNOT as the unitary operation, and to the middle 2Q operation as the not unitary A. So:

enter image description here enter image description here

Ron Cohen
  • 1,194
  • 3
  • 17