1

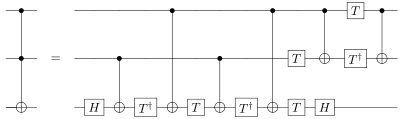
I am trying to write Toffoli gate matrice by using one and two qubit gates matrices. I follow this circuit

link for the circuit

enter image description here

I first started to write the matrices of one and two qubit gates:

identity = np.array([[1, 0], [0, 1]])
xgate = np.array([[0, 1], [1, 0]])
ygate = np.array([[0,-1j],[1j,0]])
zgate = np.array([[1,0],[0,-1+0j]])
hgate = 1/math.sqrt(2)*(xgate+zgate)
sgate = np.sqrt(zgate)
tgate = np.sqrt(sgate)
tdag = tgate.conj().T
cnot = 0.5*(np.kron(identity,identity)+np.kron(identity,xgate)+np.kron(zgate,identity)-np.kron(zgate,xgate))
deneme = np.kron(identity, swap)
deneme2 = np.kron(cnot,identity)
deneme3 = np.kron(identity,swap)
#deneme_ = deneme*deneme2*deneme3
deneme_ = np.matmul(deneme,deneme2)
non_adjacent  = np.matmul(deneme_,deneme3)

Then, I started to write each part of the circuit in the following way:

tof1 = np.kron(np.kron(identity,identity),hgate)
tof2 = np.kron(identity,cnot)
tof3 = np.kron(np.kron(identity,identity),tdag)
tof4 = non_adjacent
tof5 = np.kron(np.kron(identity,identity),tgate)
tof6 = np.kron(identity,cnot)
tof7 = np.kron(np.kron(identity,identity),tdag)
tof8 = non_adjacent
tof9 = np.kron(np.kron(identity,tdag),tgate)
tof10 = np.kron(cnot,hgate)
tof11 = np.kron(np.kron(identity,tdag),identity)
tof12 = np.kron(cnot,identity)
toffoli = tof1*tof2*tof3*tof4*tof5*tof6*tof7*tof8*tof9*tof10*tof11*tof12

And the final matrix is that: enter image description here

My guess is that: I did a mistake when I tried to write cnot gate for the first and third qubits or maybe I am wrong to write identities

Can someone explain to me what I missed? Sorry for this dumb question Thanks in advance

glS
  • 24,708
  • 5
  • 34
  • 108
quest
  • 624
  • 3
  • 9
  • Here is a "manual" how to write a matrix representing CNOT working on non-adjacent qubits (in your case tof4 and tof8 steps which you have wrong): https://quantumcomputing.stackexchange.com/questions/9180/how-do-i-write-the-matrix-for-a-cz-gate-operating-on-nonadjacent-qubits/9185#9185 – Martin Vesely Dec 28 '21 at 10:19
  • @MartinVesely thanks, I wrote swap gate and then I wrote this code lines: tof4 = np.matmul(swap,cnot) tof4 = np.kron(tof4,identity)# and I did the same for tof8 too but the result is still weird – quest Dec 28 '21 at 11:43
  • also I tried to write the matrix which is described here: https://quantumcomputing.stackexchange.com/questions/9180/how-do-i-write-the-matrix-for-a-cz-gate-operating-on-nonadjacent-qubits/9185#9185 directly but still did not work for me – quest Dec 28 '21 at 11:47
  • I see now, you have to multiply the matrices instead of summing them - Toffoli = tof13*tof12....tof1. Moreover, check again each step, I see a S gate in tof13 however the last step is CNOT acting on first and second qubits. – Martin Vesely Dec 28 '21 at 12:01
  • thanks a lot, I am now checking the code and will back to you in half hour – quest Dec 28 '21 at 12:18
  • 1
    The issue is you're using * instead of @ to combine the pieces. For numpy, * is pair-wise product, and @ is matrix multiplication. – Craig Gidney Dec 29 '21 at 00:08
  • later, I tried @ too, However I could see some very very small numbers like e-17, then I set up the writing settings and it was ok. But thanks for reminder, always confused numpy matrix stuff – quest Dec 30 '21 at 10:38

1 Answers1

1

Here I am providing working code:

import numpy as np
import math as m

idn = np.array([[1, 0], [0, 1]])


h = (1/m.sqrt(2))*np.array([[1, 1], [1, -1]])


t =    np.array([[1, 0], [0, (1/m.sqrt(2))*(1+1j)]])
tdag = np.array([[1, 0], [0, (1/m.sqrt(2))*(1-1j)]])


cnot_adj = np.array([[1, 0, 0, 0],
                     [0, 1, 0, 0],
                     [0, 0, 0, 1],
                     [0, 0, 1, 0]])


cnot_non_adj = np.array(
                        [[1, 0, 0, 0, 0, 0, 0, 0],
                         [0, 1, 0, 0, 0, 0, 0, 0],
                         [0, 0, 1, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 1, 0, 0],
                         [0, 0, 0, 0, 1, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 1],
                         [0, 0, 0, 0, 0, 0, 1, 0],
                        ]
                        )


toffoli = np.kron(np.kron(idn, idn), h)
toffoli = np.dot(np.kron(idn, cnot_adj), toffoli)
toffoli = np.dot(np.kron(np.kron(idn, idn), tdag), toffoli)
toffoli = np.dot(cnot_non_adj, toffoli)
toffoli = np.dot(np.kron(np.kron(idn, idn), t), toffoli)
toffoli = np.dot(np.kron(idn, cnot_adj), toffoli)
toffoli = np.dot(np.kron(np.kron(idn, idn), tdag), toffoli)
toffoli = np.dot(cnot_non_adj, toffoli)
toffoli = np.dot(np.kron(np.kron(idn, t), t), toffoli)
toffoli = np.dot(np.kron(cnot_adj, h), toffoli)
toffoli = np.dot(np.kron(np.kron(t, tdag), idn), toffoli)
toffoli = np.dot(np.kron(cnot_adj, idn), toffoli)


np.set_printoptions(precision=3) #"rounding"
np.set_printoptions(suppress=True) #supressing scientific format"
print('Real parts')
print(toffoli.real)
print('\nImaginary parts')
print(toffoli.imag)

Variable cnot_non_adj is CNOT gate with control on the uppermost qubit and target on the lowermost qubit. The matrix is designed according to manual I provided here.

Note that np.dot is a matrix multiplication. You can see, that the order in the multiplication is reversed in comparison with the diagram.

The result of the code is

Real parts
[[1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 1. 0.]]

Imaginary parts
[[-0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0. -0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0. -0. -0.]
 [ 0.  0.  0.  0.  0.  0. -0. -0.]]

This is a matrix description of the Toffoli gate.

Martin Vesely
  • 13,891
  • 4
  • 28
  • 65
  • 1
    Ah that is : np.set_printoptions(precision=3) #"rounding" np.set_printoptions(suppress=True) #supressing scientific format" Thank you very much now my code is also working agter your warnings. I deleted tof13 and I multiplied like you did and it is now working. Many thanks. This is great :)))) – quest Dec 28 '21 at 12:51
  • 1
    @quest: You are very welcome. I am glad I helped! – Martin Vesely Dec 28 '21 at 13:10