6

By my calculations, it looks like the SWAP gate is a Clifford Gate. See the following table:enter image description here

I follow the same method as in this paper for showing a gate is a Clifford Gate. I got the above table by performing calculations in Qiskit. How would I express the SWAP gate in terms of the generators of the Clifford group? The generators are the $H$ gate, the $S$ gate and the $CNOT$ gate.

Adam Zalcman
  • 22,278
  • 3
  • 34
  • 83
Quantum Guy 123
  • 1,371
  • 5
  • 18

3 Answers3

8

It's well known that you can make a swap out of three CNOTs.

enter image description here

For reference, Stim's gate documentation includes H+S+CX decompositions of a lot of Clifford gates including the swap:

Stabilizer Generators:

X_ -> +X
Z -> +Z
_X -> +X
Z -> +Z


Unitary Matrix:


[+1  ,     ,     ,     ]
[    ,     , +1  ,     ]
[    , +1  ,     ,     ]
[    ,     ,     , +1  ]


Decomposition (into H, S, CX, M, R):


The following circuit is equivalent (up to global phase) to SWAP 0 1


CNOT 0 1
CNOT 1 0
CNOT 0 1
Craig Gidney
  • 36,389
  • 1
  • 29
  • 95
  • thank you for the answer :) I saw before the the $C_{2}NOT_{1}$ and $C_{1}NOT_{2}$ gates can be used to make a $SWAP$ gate. My question then is: how is the $C_{2}NOT_{1}$ generated using the generators of the Clifford group? – Quantum Guy 123 Nov 11 '21 at 18:24
  • 1
    $C_2NOT_1=(H\otimes H)\circ C_1NOT_2\circ(H\otimes H)$ – Adam Zalcman Nov 11 '21 at 18:26
  • 1
    @QuantumGuy123 That gate is considered to be in the gate set. But if you really want to go out of your way you can just surround a CNOT with Hs instead of switching the target and control roles. – Craig Gidney Nov 11 '21 at 18:26
  • hey @CraigGidney, do you (or perhaps someone you know) know the answer to my other question on Cliffords?: https://quantumcomputing.stackexchange.com/questions/21993/does-a-pauli-being-acted-on-by-a-random-clifford-get-sent-to-every-pauli-with-eq – Quantum Guy 123 Nov 19 '21 at 22:14
4

Yes, SWAP is a Clifford gate.

Your proof is correct. By definition, an $n$-qubit gate $U$ is Clifford if $UPU^\dagger\in G_n$ for all $P\in G_n$ where $G_n$ is the $n$-qubit Pauli group. However, it is easy to see that we only need to check that $UQU^\dagger\in G_n$ for $Q$ that are generators of $G_n$. Moreover, $G_n$ is generated by $\{i, Z_k, X_k\,|\,k=1,\dots,n\}$ where $X_k$ denotes the tensor product of Pauli $X$ on the $k$th qubit and identity applied to all other qubits and similarly for $Z_k$. Since $UiU^\dagger=iI\in G_n$ for all $U$, we only have to check that $UX_kU^\dagger\in G_n$ and $UZ_kU^\dagger\in G_n$ for $k=1,\dots,n$. This is exactly what the table in the question accomplishes.

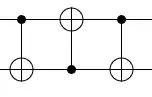
It is easy to check that

$$ \text{SWAP} = C_1NOT_2 \circ C_2NOT_1 \circ C_1NOT_2\tag1 $$

where $C_iNOT_j$ denotes the CNOT gate with qubit $i$ as control and $j$ as the target, e.g. by applying both sides of $(1)$ to the computational basis states.

Adam Zalcman
  • 22,278
  • 3
  • 34
  • 83
3

Perhaps might be of interest to provide a full proof that the SWAP operation is equal to the $3$ CNOT gates described in the other answers. A very interesting way to prove this is using the ZX-calculus. We only need the following re-writing rules, known as (1) the bialgebra rule and (2) the Hopf rule.

Equation (1):

enter image description here

Equation (2):

enter image description here

The proof is taken from this reference.

First, translate the circuit description in terms of the calculus,

enter image description here

Now, using the fact that maintaining the connectivity one can change freely the diagram we have the following equations:

enter image description here

Which concludes the proof. Apart from the non-trivial rules we also used fusion of spiders and that the white or grey circles as gates are equivalent representations of the identity.

R.W
  • 2,337
  • 6
  • 25