You can simply teleport a state per partes, i.e. each qubit separately.
To do so, firstly you have to prepare as many Bell states as a number of qubits teleported. Then entangle each qubit of the teleported state with your part of some Bell state and run the protocol to teleport the qubit to other side. This has to be done for each qubit of the teleported state.
Here is an example of teleporting two-qubits entangled state $\cos(\pi/8)|01\rangle + \sin(\pi/8)|10\rangle$:
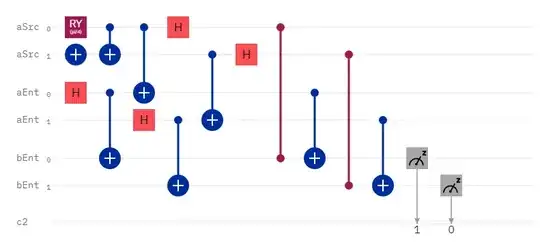
Here is a commented code in QASM for the circuit above
OPENQASM 2.0;
include "qelib1.inc";
qreg aSrc[2];
qreg aEnt[2];
qreg bEnt[2];
creg c[2];
//teleported state psi prep.
ry(pi/4) aSrc[0];
x aSrc[1];
cx aSrc[0],aSrc[1];
//entangling Alice and Bob
h aEnt[0]; //first qubit
cx aEnt[0],bEnt[0];
h aEnt[1]; //second qubit
cx aEnt[1],bEnt[1];
//connecting psi to quantum channel
//between Alice and Bob
cx aSrc[0],aEnt[0]; //first qubit
h aSrc[0];
cx aSrc[1],aEnt[1]; //secpmd qubit
h aSrc[1];
//sending classical bits - teleport.
//(here used q-gates for
//the circuit simplification)
cz aSrc[0],bEnt[0];//first qubit
cx aEnt[0],bEnt[0];
cz aSrc[1],bEnt[1];//second qubit
cx aEnt[1],bEnt[1];
//measurement at Bob
measure bEnt[0] -> c[1];
measure bEnt[1] -> c[0];
And finally here are results of the teleportation on IBM Quantum simulator (1024 shots):
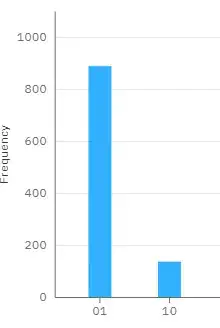
Clearly, you can extend this approach to general $n$-qubits state. To be honest, I do not know if this approach is the most efficient in terms of Bell states used.
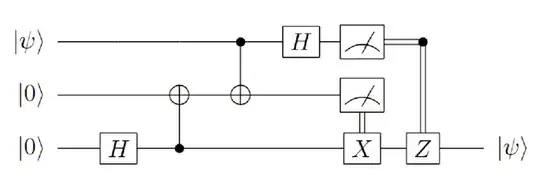 How easy is to generalize this algorithm to allow for the teleportation of the state of 2 or $n$-qubits?
How easy is to generalize this algorithm to allow for the teleportation of the state of 2 or $n$-qubits?
