How to combine/calculate for interference using density matrices?

Question

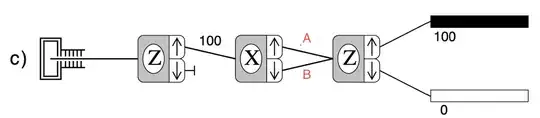
Let's assume following two density matrices are corresponding to the A and B in the Stern-Gerlach apparatus bellow (I know Stern-Gerlach is a more of a physics experiment but I think it can equally be considered a quantum computing problem):

$\rho_A=\frac{1}{2}\begin{pmatrix}1&1\\1&1\end{pmatrix}$

$\rho_{B}=\frac{1}{2}\begin{pmatrix}1&-1\\-1&1\end{pmatrix}$

We also have the following two projection operators:

$p_{z+}=\begin{pmatrix}1&0\\0&0\end{pmatrix}$

$p_{z-}=\begin{pmatrix}0&0\\0&1\end{pmatrix}$

In such case how should we calculate and combine the density matrices to find out the very last Z device output?

It seems to me that the result has to be $\begin{pmatrix}1&0\\0&0\end{pmatrix}$, but I don't know how this calculation has to be done so that it takes into account the interference, in a coherent way!

Answer 1

By definition a density matrix is given by:

$$\rho= \sum p_i |\psi_i \rangle \langle \psi_i|$$

Where there is a probability $p_i$ of finding the state to be $|\psi_i\rangle$. Now if we are "combining" two quantum states represented by $\rho_A= \sum p_{A_i} |\psi_i \rangle \langle \psi_i|$ and $\rho_B= \sum p_{B_i} |\psi_i \rangle \langle \psi_i|$ then the "combined" state will be found in state $|\psi_i\rangle$ with probability $\frac{p_{A_i}+p_{B_i}}{2}$. This follows from directly from basic probability. And so the combined density matrix will be given by:

$$\rho_{A+B}= \sum \frac{p_{A_i}+p_{B_i}}{2} |\psi_i \rangle \langle \psi_i|$$

It seems that you already somewhat realize this, but the analysis that follows from what you laid out obtains the wrong result, and this is because the projection operators you defined are not accurate for what is happening. We do not in fact have two independent quantum states $\rho_a$ and $\rho_b$ being "combined" but what is happening is a little more subtle.

From the input of the $X$ measurement to the input of $Z$ measurement we do indeed have $P_{z+}$ and $P_{z-}$, but because we never collapse our state and just recombine them after the $Z$ measurement, the net effect of that gate and the recombination is given by $P_{z+}+P_{z-}=\mathbb{1}$. And so the objects you defined in the question as $\rho_a$ and $\rho_b$ never actually exist. Infact at the input of the $Z$ measurement our state is given by:

$$\big(P_{z+}+P_{z-} \big)| z+\rangle=| z+\rangle$$

And correspondingly we measure $100\%$ of spins to be positive in the $z$ basis

Answer 2

Perhaps I am misunderstanding the question, but I don't agree that you get one measurement result with 100% probability.

Let me run through the calculation first with pure states (as much as I can!).

We start on the left of the diagram, and when the particles pass through the first measurement device, we are selecting the $|z+\rangle$ state by blocking the $|z-\rangle$ output. We express $$ |z+\rangle=\frac{1}{\sqrt{2}}(|x+\rangle+|x-\rangle) $$ so that tells us that if we measure using the $x$ basis (the next step), the outcomes are 50:50. Let us now recombine the two outputs so that we cannot tell which measurement result we got. We're forced to already use the density matrix formalism at this point. The output from the $x$ measurement (and recombining of paths) is $$ \frac12|x+\rangle\langle x+|+\frac12|x-\rangle\langle x-|=I/2. $$ This is the state that is input to the final $Z$ measurement on the right-hand side. Clearly, you get 50:50 outcomes.

The density matrix analysis is exactly the same. We start with $$ \rho=P_{z+}. $$ The probabilities of measurement outcomes $x\pm$ are $\langle x\pm|\rho|x\pm\rangle=\frac12$ and the corresponding outcome states are $P_{x\pm}$, and so the net state after we've recombined the two outcomes is $$ \frac12(P_{x+}+P_{x-})=I/2 $$ and analysis of the final measurement is exactly the same as before because it's the same formalism.

If you look, for example, at Figure 6.9 in http://physics.mq.edu.au/~jcresser/Phys301/Chapters/Chapter6.pdf this agrees with my analysis.