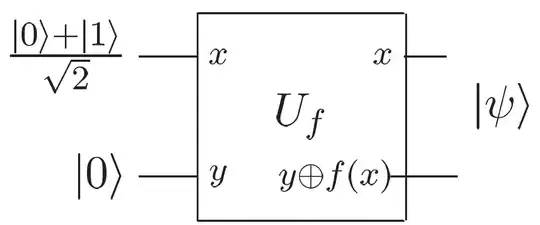Intuition for why the normalization for states in quantum parallelism is the same

Question

On page 31 of Quantum Computation and Quantum information by Nielsen and Chuang, it is said that:

Consider the circuit shown in Figure 1.17, which applies $U_f$ to an input not in the computational basis. Instead, the data register is prepared in the superposition $\frac1{\sqrt2}(|0\rangle+|1\rangle)$, which can be created with a Hadamard gate acting on $|0\rangle$. Then we apply $U_f$, resulting in the state: $\frac1{\sqrt2}(|0,f(0)\rangle+|1,f(1)\rangle)$.

I'm curious why the normalization for the second state, $\frac1{\sqrt2}(|0,f(0)\rangle+|1,f(1)\rangle)$, is also $\frac1{\sqrt2}$. And what's the intuition behind this?

Answer 1

$U_f$ is defined as $U_f: |x\rangle|y\rangle \rightarrow |x\rangle|y\oplus f(x)\rangle$. Now, let's write the product state of the complete system of two qubits before applying $U_f$. We can do this with tensor products as follows:

$$ \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes |0\rangle = \frac{1}{\sqrt{2}}(|0\rangle\otimes|0\rangle + |1\rangle\otimes|0\rangle) = \frac{1}{\sqrt{2}}(|00\rangle + |10\rangle) $$

As you can see, the scalar $\frac{1}{\sqrt{2}}$ doesn't affect the tensor product itself and just remains there as a constant. This may be easier to see when considering kets in their vector form and the Kronecker product:

$$ \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 0 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0\end{bmatrix} $$

These two derivations are equivalent, but as you can see the first one is way simpler although in the second one it may be easier to see how the amplitude is conserved.

Now, we haven't applied $U_f$ yet. To do this, we will work with the ket representation of our state since that is how the unitary is defined. So, applying $U_f$ looks as:

$$ U_f\left[\frac{1}{\sqrt{2}}(|00\rangle + |10\rangle)\right] = \frac{1}{\sqrt{2}}(U_f|00\rangle + U_f|10\rangle) = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) $$

We could do the first step since most operators in quantum computing are linear, meaning that $f(x+y)=f(x)+f(y)$ for an operator $f$. Using this derivation we can see that the amplitude of $\frac{1}{\sqrt{2}}$ is conserved throghout the whole computation.

For the intuition, remember that the squared norm of your statevector must always be equal to one, in other words, the sum of the amplitudes squared of your state needs to be $1$ at all points in the computation since this represents the probability of the system to be in a certain state, and these probabilities always need to sum to $1$.

Another thing to note is that most quantum operators are unitary (in this case $U_f$ is unitary). Meaning that these operators preserve the norm constraint I talked about in the last paragraph. To read more about unitary and other types of operators, I recommend looking at the answers to this question.

Answer 2

On the last few lines at page 30 (Nielsen and Chuang section 1.4.2) is stated: "Suppose $f(x) : \{0,1\} \to \{0,1\}$ is a function with one bit domain and range". So, the value of $f(x) $ is only either 0 or 1 (a single bit), for every $x$. $U_f$ is just a gate to achieve the transformation $y \oplus f(x)$ in the ancillary qubit. Now consider one particular case where $f(0) = 1$ and $f(1) = 0$. Then, in this case, going by what the book says, the output state takes the form $\frac{|{01}\rangle+|{10}\rangle}{\sqrt{2}}$. It is easy to see that the normalization factor for this 2 qubit state is correct. Similarly for all other possible values of $f$.