Based on the paper Elementary gates of ternary quantum logic circuit, the extensions of the Z gate are as follows
$$
\begin{gather}
Z^{[0]} = \text{diag}\{-1, I_2\} = \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\
Z^{[1]} = \text{diag}\{1, -1, 1\} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\
Z^{[2]} = \text{diag}\{I_2,-1\} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix}
\end{gather}
$$
The controlled variant, denoted $TCZ$, is defined as the gate that implements $Z^{[n']}$ on the target qutrit iff the control qutrit is in the state $|n\rangle$ where $n\in\{0, 1, 2\}$. Figure 3 (a) below gives the circuit representation of the $TCZ$ gate.
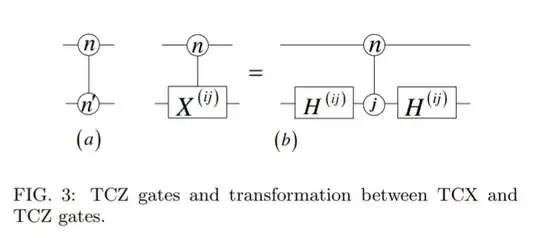
However, as noted in the comments by @unknown, this gates are not Clifford. For a Clifford formulation of the $Z$ gate, we can turn to Canonical forms for single-qutrit Clifford+T operators that defines it as
$$
Z = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \omega & 0 \\ 0 & 0 & \omega^2 \end{bmatrix},
$$
with $\omega = e^{2 \pi i / 3}$ which means $Z^3=I$. To convert this into a qutrit controlled-$Z$ operator, I recommend taking a look at this answer, taken from a question linked in the comment to your original question.
