How do successive operators act in the Heisenberg picture?

Question

In the Schrodinger picture, it is clear how write a single gate for two operators. For example if operators $A$ then $B$ act on a state $\vert \psi \rangle$, this gives $BA\vert \psi \rangle$, (noting that the operator that acted last is written first). This could of course be written as a single operator $BA$.

In a circuit diagram we would have:

However in the Heisenberg picture (for the same circuit), the state would remain unchanged and the operators would evolve:

Now in order for these two operators to product into the same operator as in the Schrodinger case, we now need to write the operator that acted first acting first so that the $A^{\dagger}$ and $A$ cancel out.

1. Is this the correct interpretation of each picture and the way of translating between the two pictures?

2. Why does the order in which we write the operators change/appear to change in each picture?

Answer 1

The point of the Heisenberg picture is that, instead of considering the time-evolution of a state, you "evolve backward in time" the operator describing the measurement.

We can describe the most general possible setting as follows: let $\rho$ be some state (in the density matrix formalism), let $\Phi$ be some quantum channel, and let ${\cal O}$ be some observable. The expectation value of $\mathcal O$ when measuring $\rho$ after evolution through $\Phi$ is $$\langle\mathcal O\rangle_{\Phi(\rho)}\equiv \langle\mathcal O,\Phi(\rho)\rangle \equiv \operatorname{Tr}[\mathcal O \Phi(\rho)].$$ The corresponding "Heisenberg picture" is obtained evolving instead the observable $\mathcal O$ back in time, thus obtaining some "effective observable" $\mathcal O'$ which, when measured on $\rho$, gives the same result as measuring $\mathcal O$ on $\Phi(\rho)$. More precisely, you get this defining $\mathcal O'=\Phi^\dagger(\mathcal O)$, where $\Phi^\dagger$ denotes the adjoint of the channel $\Phi$. These two descriptions are equivalent because, by the definition of the adjoint, we have $$\operatorname{Tr}[\mathcal O\Phi(\rho)] \equiv \langle \mathcal O,\Phi(\rho)\rangle = \langle \Phi^\dagger(\mathcal O),\rho\rangle \equiv \operatorname{Tr}[\Phi^\dagger(\mathcal O)\rho].$$

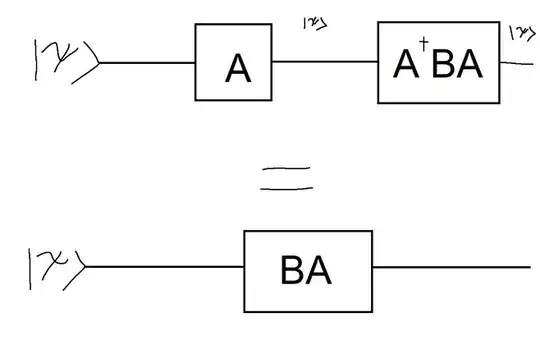
One point worth stressing is that in the Heisenberg picture you evolve back observables, not channels (or, in your case, gates). The gates in your picture, and more generally the evolution operators, are what defines the dynamics, and thus describe evolution in Schrodinger's, Heisenberg's, or any other picture. But what evolves are states, or observables.

To specialise the above general setting to the case of a unitary dynamics with pure states and projective measurements, consider an initial state $|\psi\rangle$, a unitary gate $U$, and a projective measurement on a state $|\phi\rangle$. Then you have $$|\langle\phi| U |\psi\rangle|^2 \equiv \operatorname{Tr}[(U^\dagger |\phi\rangle\!\langle\phi| U)\, |\psi\rangle\!\langle\psi|],$$ where the LHS is how you normally describe measuring the output of the circuit, and the RHS the way you'd describe it in the corresponding "Heisenberg picture". Again, let me stress that here $U$ takes the role of $BA$ in your picture.

Finally, to more directly address the titular question: sequences of evolution operations translate in the Heisenberg picture as sequences of their adjoints in inverse order. This is a straightforward property of the adjoint operation: for any two channels $\Phi,\Psi$, we have $(\Psi\circ\Phi)^\dagger=\Phi^\dagger\circ\Psi^\dagger$. Or in the unitary formalism with gates, you have $$|\langle\phi| BA |\psi\rangle|^2 \equiv \operatorname{Tr}[(A^\dagger B^\dagger |\phi\rangle\!\langle\phi| BA)\, |\psi\rangle\!\langle\psi|].$$