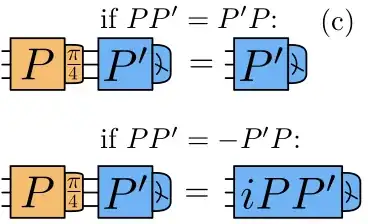How to reason about absorbing Pauli Product rotations into measurements?

Question

In this image, the orange box refers to the operator $\exp(-i P \frac{\pi}{4})$ and the blue box refers to the Pauli Measurement $P'$. The idea behind these rules is to show how all the Pauli Product $\frac{\pi}{4}$ rotations at the end of the circuit can be absorbed into the measurements.

How would you prove these equations? In particular, I am looking for a proof that will help me reason about what happens if I measure say just the first qubit after performing a multi qubit orange box. For example, how would I absorb the orange box into the measurements in the following?

Markus Heinrich · Accepted Answer · 2021-03-25T15:32:52.373

First of all, let us consider an arbitrary unitary $U$. If we first apply $U$ and then measure a POVM $\{E_a\}$, then this is equivalent to doing nothing and measuring the POVM $\{U^\dagger E_a U\}$ instead since $\mathrm{Pr}[a|\rho] = \mathrm{tr}\left( E_aU \rho U^\dagger \right) = \mathrm{tr}\left( U^\dagger E_a U \rho \right)$. In particular, a Pauli measurement is given by the projectors $\frac 1 2 \left( \mathbb{I} \pm P \right)$ and the altered measurement is described by the Hermitian operator $O = U^\dagger P U$.

Now note that $U=\exp(- i\frac \pi 4 P)$ is a Clifford unitary if $P$ is a Pauli operator. Thus, absorbing the action of $U$ into the measurement of a Pauli operator $Q$ will result in another Pauli measurement of $\pm Q'=U^\dagger Q U$. Note that the possible sign simply relabels the outcomes. Next, it is clear that $U^\dagger Q U=Q$ if $P$ and $Q$ commute, thus we can remove $U$ from the circuit. If not, a straightforward calculation shows that $$ e^{i\frac \pi 4 P}Qe^{- i\frac \pi 4 P} = i PQ \equiv \pm Q'. $$

If you measure the first qubit after a $n$-qubit Clifford gate, than this effectively the same as doing nothing and performing a Pauli measurement on many ($\leq n$) qubits (since $U$ will generally map a Pauli operator on the first qubit to a Pauli operator supported on $n$ qubits).

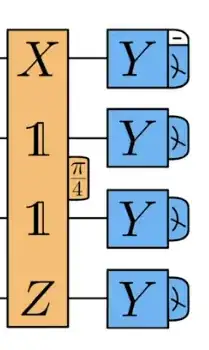
The measurement in your final example consists of measuring four commuting Pauli operators $P_1,\dots,P_4$ (a syndrome measurement). The projectors of the joint measurement are given as products $P_x = \prod_{i=1}^4 \frac 1 2 (\mathbb I + (-1)^{x_i} P_i)$ where $x\in \{0,1\}^4$. To compute $UP_x U^\dagger$, we can thus individually transform the involved projectors.

Let us use the above reasoning sequentially:

$X\otimes\mathbb{I}\otimes\mathbb{I}\otimes Z$ anti-commutes with $Y\otimes\mathbb{I}\otimes\mathbb{I}\otimes\mathbb{I}$, thus we can replace the measurement of $-Y$ on the first qubit by the measurement of $-iXY\otimes\mathbb{I}\otimes\mathbb{I}\otimes Z=Z\otimes\mathbb{I}\otimes\mathbb{I}\otimes Z$.
The Pauli operators on the second and third qubit obviously commute with the unitary, so the measurements are unchanged.
The last Pauli operator again anti-commutes, so we can replace it by the measurement of $X\otimes\mathbb{I}\otimes\mathbb{I}\otimes i ZY=X\otimes\mathbb{I}\otimes\mathbb{I}\otimes X$.

Note that we obtained an entangling measurement between the first and the fourth qubit. This is in fact a Bell measurement as the joint eigenvectors of $X\otimes X$ and $Z\otimes Z$ are the four Bell states $\{|00\rangle \pm |11\rangle, |01\rangle \pm |10\rangle\}$.

Hi, I'm still trying to work through understanding your answer but just from my partial understanding so far, might you have assumed that the measurement in the example circuit was a Pauli YYYY measurement? It is in fact 4 distinct single qubit measurements, sorry if this wasn't clear. The first is -Y , the other three are Y. — shashvat, Mar 24 '21 at 18:00
@user3717194 I see, sorry for that. Anyway, you can still argue similarly, I'll update the answer. — Markus Heinrich, Mar 25 '21 at 15:03

score 0 · Answer 2 · answered Mar 25 '21 at 15:52

Here's a sort of simple way to do it, if you have a simulator you trust. Note that a Z-basis measurement is equivalent to a Z-controlled CNOT onto an ancilla qubit and then measuring that ancilla in the Z basis. And that a Y-basis measurement is equivalent to a Y-controlled CNOT onto an ancilla qubit and then measuring that ancilla in the Z basis.

What you can do is assert that moving the rotation before the controlled operation changes the control basis of the controlled operation:

import stim
sim1 = stim.TableauSimulator()
sim1.do(stim.Circuit("""
    SQRT_X 0
    CNOT 0 99  # 99 is the ancilla where we're putting the measurement result
"""))
sim2 = stim.TableauSimulator()
sim2.do(stim.Circuit("""
    YCX 0 99  # Y-controlled X gate
    SQRT_X 0
"""))
assert sim1.current_inverse_tableau() == sim2.current_inverse_tableau()

To be safe, you likely want to use the state channel duality to ensure the simulation works for all states instead of just one state.

import stim
sim1 = stim.TableauSimulator()
sim1.do(stim.Circuit("""
    H 0
    CNOT 0 98  # 98 is the state channel ancilla
SQRT_X 0
CNOT 0 99  # 99 is the ancilla where we're putting the measurement result

"""))
sim2 = stim.TableauSimulator()
sim2.do(stim.Circuit("""
    H 0
    CNOT 0 98  # 98 is the state channel ancilla
YCX 0 99  # Y-controlled X gate
SQRT_X 0

"""))
assert sim1.current_inverse_tableau() == sim2.current_inverse_tableau()

How to reason about absorbing Pauli Product rotations into measurements?

2 Answers2