2

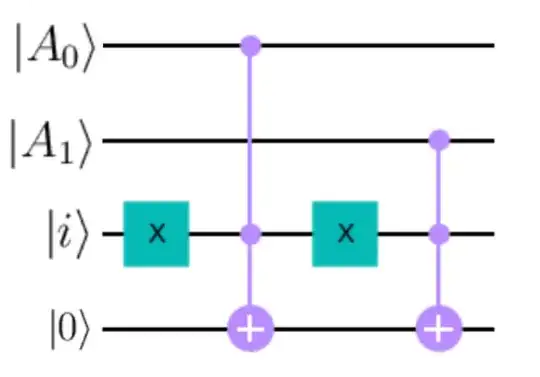
Let's assume I have two qubits of state $|A_0\rangle$ and $|A_1\rangle$ correspondingly stored in a quantum memory. How do I find a Unitary $U$ that acts on another register of 2-qubits such that $$U:|i\rangle|0\rangle\rightarrow|i\rangle|A_i\rangle?$$

Is such a unitary even possible or is this forbidden due to the no-cloning theorem? However, I don't want to clone the states $|A_0\rangle$ and $|A_1\rangle$, but rather do some kind of multiplexing with them.

That's what my register looks like:

enter image description here

In the end, I want to turn the $|0\rangle$ qubit into $|A_i\rangle$ depending on the state of the $|i\rangle$ qubit. Is something like this generally possible?

glS
  • 24,708
  • 5
  • 34
  • 108
Thomas
  • 279
  • 2
  • 10
  • 2
    I should have clarified that. I'm looking for a circuit model of the above-mentioned Unitary, so the decomposition in terms of elementary gates is what I would need. – Thomas Mar 05 '21 at 11:21

3 Answers3

7

No, this is impossible, because it violates the no-cloning theorem. You want to implement the function $$ |A_0\rangle|A_1\rangle|i\rangle|0\rangle \mapsto |A_0\rangle|A_1\rangle|i\rangle|A_i\rangle, $$ but if you could do that you could also clone, e.g. by fixing $i=0$, which would make the function be $$ |A_0\rangle|A_1\rangle|i\rangle|0\rangle \mapsto |A_0\rangle|A_1\rangle|0\rangle|A_0\rangle, $$ which is cloning the state $|A_0\rangle$ and ignoring the state $|A_1\rangle$.

Mateus Araújo
  • 2,472
  • 6
  • 16
0

Yeah you can do it! Here's the circuit:

enter image description here

The reason that the no-cloning theorem does not apply here is because you are requiring precise inputs (in particular you are choosing your input qubit to be $|0\rangle$). A cloning would look like $|A_i\rangle|i\rangle|x\rangle \rightarrow |A_i\rangle|i\rangle|A_i\rangle$ for some arbitrary $x$ which would indeed be impossible.

Also if you would like the gates to be even more 'elementary', you can check you this paper that describes how to construct CCNOT gates out of T gates.

Edit: This only works if $A_i = \{0,1\}$, not for any arbitrary superposition (thank you Mateus Araújo for pointing that out)

sheesymcdeezy
  • 1,746
  • 6
  • 25
  • Thanks a lot! That produced the expected outcome for my code! Can you maybe elaborate a little bit on your reasoning behind the gate choices? I still struggle most to find the gate decomposition if I see a general unitary like $U:|\psi\rangle\rightarrow |\phi\rangle$. – Thomas Mar 05 '21 at 12:44
  • 1
    I don't have a great intution on general unitary decomposition but I can comment about this specific one. First you want to ensure that 'if $i=1$, copy $A_1$'. That's always just a CCNOT gate (the final gate in the circuit). The other case was 'if $i=0$, copy $A_0$'. For any 'if $i=0$' statement, you can apply an $X$ gate on $|i\rangle$, use ctrl gates, and apply $X$ again.This was what was done first in the circuit. – sheesymcdeezy Mar 05 '21 at 12:55
  • 6
    No, this is completely wrong. The circuit only works if $|A_i\rangle$ is either $|0\rangle$ or $|1\rangle$. If you let it be $|+\rangle$ it will fail, for example. And the reason it cannot work is precisely that it would violate the no-cloning theorem. – Mateus Araújo Mar 05 '21 at 13:00
  • Okay, now I'm wondering why my code still returns the expected behavior. In my case, $|A_i\rangle$ is a generic state in a random superposition. – Thomas Mar 05 '21 at 14:58
  • @MateusAraújo: I am a little bit confused. I understand that the proposed circuit is in fact controlled fan-out which is used for "copying" qubits. Of course these qubits are not independend since $CNOT(\alpha|0\rangle+\beta|1\rangle)|0\rangle = \alpha|00\rangle + \beta|11\rangle$. The proposed circuit works in the same manner but the fan-out is controlled by register $|i\rangle$. So, I do not understand what is wrong. – Martin Vesely Mar 06 '21 at 08:20
  • 1
    @Thommy257: I tried to construct the propsed circuit and it works for general state. See my explanation in comment above and answer below. – Martin Vesely Mar 06 '21 at 08:39
  • 2
    The probability of measuring 1 in the last qubit is $|\beta|^2$ in both cases. You'll see a difference when measuring in a basis other than the computational one. For example, if $|A_0\rangle = |+\rangle$, and you measure the last qubit in the X basis, the circuit will give 1 with probability 1/2, but it should give 1 with probability 1 if it was doing what the question asked. – Mateus Araújo Mar 07 '21 at 11:01
0

I tried to run circuit proposed by Rajiv on IBM Q. In my case $|A_0\rangle = |+\rangle$, so probabilities of measuring 0 and 1 are 50 %. Then I set $|A_1\rangle = Ry(\pi/4)|0\rangle$ which means that probability of measuring 0 is 85 % and for 1 it is 15 %.

For setting $|i\rangle$ to $|0\rangle$, state $|A_0\rangle$ is returned to qubit $q_3$ and for setting $|i\rangle$ to $|1\rangle$, state $|A_1\rangle$ is returned to qubit $q_3$. Or in other words, I measured above mentioned probabilities on qubit $q_3$ for both settings of $|i\rangle$.

Here is a code:

OPENQASM 2.0;
include "qelib1.inc";

qreg q[4];
creg c[1];


h q[0];
ry(pi/4) q[1];
x q[2]; \put x for i = 1, remove this line for i = 0
x q[2];
ccx q[0],q[2],q[3];
x q[2];
ccx q[1],q[2],q[3];
measure q[3] -> c[0];

Concerning the no-cloning theorem. There is no violation of the theorem as the circuit proposed by Rajiv uses controled fan-outs which does not violate the theorem. See explanation here.

EDIT: Original state $A_i$ and its "copy" are of course entangled and hence not independent as the "copy" is produced by fan-out.

Martin Vesely
  • 13,891
  • 4
  • 28
  • 65
  • 2
    Rajiv's circuit does not violate the no-cloning theorem simply because it is a valid quantum circuit, anything that can actually be done within quantum mechanics cannot violate the no-cloning theorem. The problem it that it does not do what the question asked, mapping $|A_0\rangle|A_1\rangle|i\rangle|0\rangle$ to $|A_0\rangle|A_1\rangle|i\rangle|A_i\rangle$. – Mateus Araújo Mar 07 '21 at 11:04
  • @MateusAraújo: I see what you mean now. You can use the circuit by Rajiv but of course you cannot have two independent instances of $A_i$. They are entangled because they are produced by fan-out. – Martin Vesely Mar 08 '21 at 07:00