I just want to do a whole adiabatic calculation on quantum circuit. To prepare two Hamiltonian of $H_{initial}$ and $H_{classical}$ and solve $H_{classical}$ using adiabatic calc like quantum annealing.
The schedule is $H_s = (1-s/T)*H_{initial} + s/T*H_{classial}$
the time evolution operator is $e^{-iHt}$
Is the "$s$" on the schedule and the "$t$" in the operator related to each other?
Yes, it is related, although you want to be careful. Strictly, $s$ is a function of time. This gives you the possibility to vary $\frac{ds}{dt}$ based on the gap $\delta_s$ between the ground and first excited states of $H_s$, and therefore control the accuracy of your adiabatic approximation. It's up to you how you pick it, but IIRC, it's nice to have $$ \frac{ds}{dt}\sim\frac{1}{\delta_s}. $$
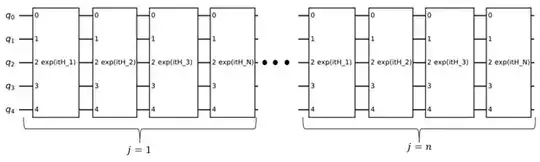
So, yes, $s$ is function of time. However, you can no longer think of the evolution as $e^{-iHt}$ because that formula only applies if $H$ is independent of time, which $H_s$ now isn't. Instead, you have to go back to the Schrödinger equation $$ \frac{d|\psi\rangle}{dt}=-iH_s|\psi\rangle $$ and solve it. A reasonable approximation can be arrived at by thinking that $H_s$ is approximately constant over a set of intervals $\delta t_i$ so that you get a product $$ \approx e^{-iH_{s_N}\delta t_N}\ldots e^{-iH_{s_2}\delta t_2} e^{-iH_{s_1}\delta t_1}. $$
If you have a Hermitian matrix, Hamiltonian, of the form $H = \sum_i H_i$. Then we can approximate $e^{-iHt}$ as follows:
$$ e^{-iHt} \approx \prod_{j=1}^n \prod_i e^{-iH_i t/n} $$
This approximation is a consequence of the Trotter product or also known as Lie product formula.
Now in term quantum circuit, it will be something like:
Then you somehow need to decompose each of the operator $e^{itH_i}$ into elementary gates. To do this step, look at this paper here: Simulation of Electronic Structure Hamiltonians UsingQuantum Computers. This answer by Davit is also really good reference to look at.
