How can I convert exponentials of pauli matrices to circuits of this form in Qiskit?

Question

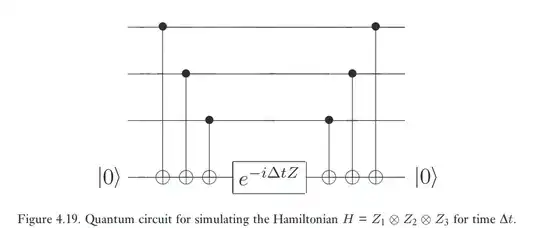
For example the following circuit is for $e^{-i(Z\otimes Z\otimes Z)\Delta t} $

I know this can even be done without the ancilla qubit, having the CNOTs control the last qubit and applying an RZ on the last qubit. Also, if instead of only Zs, our Pauli matrix is any combination of $I$,$X$,$Y$ and $Z$, we can still have it in this sort of format by swapping the $X-Z$ or $Y-Z$ bases before and after the circuit shown above.

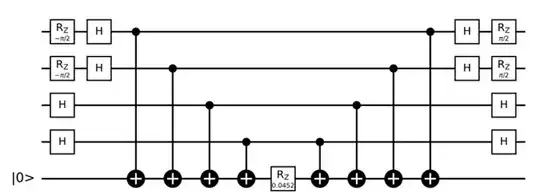
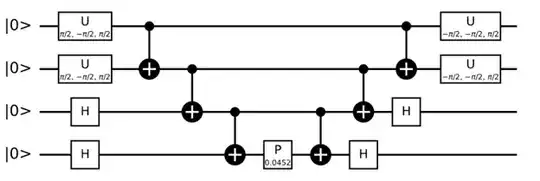
So if I have an operator like $e^{-i 0.022616399973028944 YYXX}$, in Qiskit, how I can make this into a circuit of this kind of form? I am looking for a function that does this for a general operator of this form. Is there such a function in Qiskit?

Some similar threads: https://quantumcomputing.stackexchange.com/questions/5567/circuit-construction-for-hamiltonian-simulation/11373#11373, https://quantumcomputing.stackexchange.com/questions/11663/how-to-convert-qubo-problem-to-ising-hamiltonian and https://quantumcomputing.stackexchange.com/questions/12001/how-to-build-a-circuit-for-simulation-of-a-simple-hamiltonian — Martin Vesely, Feb 19 '21 at 07:51
It is possible in Microsoft: https://docs.microsoft.com/en-us/qsharp/api/qsharp/microsoft.quantum.intrinsic.exp There you can Take Pauli Operators, and transform them into analog circuit — Ron Cohen, Dec 06 '21 at 08:21

KAJ226 · Answer 1 · 2021-02-19T05:46:32.167

3

How about:

Note that $X = HZH$ and $Y= R_Z(-\pi/2) H Z H R_Z(\pi/2)$.

In term of is there a way to do this automatically in qiskit, I don't think there is a way to do this for general case in qiskit... but I might be wrong. My best bet is you will have to write your own function to do this automatically. It shouldn't be too much of a task.

If you want to do it without the ancilla qubit case like you mentioned in your question, then you can use WeightedPauliOperator from qiskit.

For example:

pauli_dict = {'paulis': [{"coeff": {"imag": 0, "real": 0.04523/2 }, "label": "XXYY"}]}
operator = WeightedPauliOperator.from_dict(pauli_dict)
circuit = operator.evolve(evo_time= 1, num_time_slices=1).decompose()
circuit.draw( 'mpl',style={'name': 'bw'}, plot_barriers= False, initial_state = True, scale = 1)

will generate the circuit:

edited Feb 19 '21 at 05:46

answered Feb 19 '21 at 05:19

KAJ226

13,822
2
10
30

Hi, thank you for sharing the circuit, this is exactly what I want to produce. I am looking for how I can do this using code in Qiskit – shashvat Feb 19 '21 at 05:25
1

Do you want to do it in general case or just specifically? If it is general, then you want to write a function to do such thing automatically. – KAJ226 Feb 19 '21 at 05:29
Yes general case. Is there any helper function already in Qiskit? (Otherwise, I've just written up my own implementation already) – shashvat Feb 19 '21 at 05:29
I see. I don't think there is a function within qiskit to do this. If you don't want to use ancilla case then there is a way through operator.evolve() but I guess you have to write your own function... sorry to misunderstood your point earlier. – KAJ226 Feb 19 '21 at 05:33

viwosh · Answer 2 · 2021-02-25T16:41:21.860

3

You can try,

from qiskit.quantum_info import Operator
from qiskit.extensions import HamiltonianGate
create tensor of single-qubit operators. Recognized labels are
I, X, Y, Z, H, S, T, 0, 1, +, -, r, l
op = Operator.from_label('ZZZ')
create gate which evolves according to exp(-iop0.02)
gate = HamiltonianGate(op, 0.02)
circuit = QuantumCircuit(3)
apply gate to qubits [0, 1, 2] in circuit
circuit.append(gate, [0, 1, 2])

edited Feb 25 '21 at 16:41

answered Feb 20 '21 at 00:21

viwosh

51
2

1

Hi and welcome to Quantum Computing SE. Please add some details how the code works (e.g. add comment to each line what it does). – Martin Vesely Feb 20 '21 at 07:26
Nice! looks like they added the feature now? – shashvat Dec 06 '21 at 09:21

How can I convert exponentials of pauli matrices to circuits of this form in Qiskit?

2 Answers2

create tensor of single-qubit operators. Recognized labels are

I, X, Y, Z, H, S, T, 0, 1, +, -, r, l

create gate which evolves according to exp(-iop0.02)

apply gate to qubits [0, 1, 2] in circuit