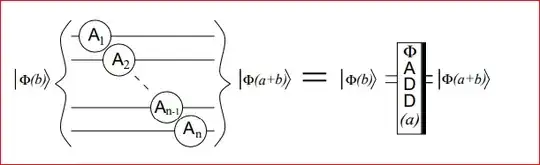
I am currently reading Shor's algorithm on my own and I come across a paper via this link. It shows the circuit for implementing Shor's alogrithm. Here it depicts that taking a QFT circuit on the number a on the qubits b that are already in fourier space would result in the addition of a and b in Fourier space.
The addition is quite intuitive. However, when it comes the subtraction, I am stuck.Why taking an inverse QFT circuit would result in the $b-a$ or $2^{n+1} - (a-b)$? Wouldn't it return $a+b$ as the second stage output is $\Phi(a+b)$?