Decomposition of 2-qubit Hamiltonian into standard gate set for QAOA

Question

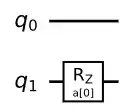
I try to decompose ansatz into gate set in order to create a circuit in qiskit for QAOA algorithm. I don't understand how represent parametrized 2 qubit ansatz as circuit.

$ H{_B} = \sum_{j=1}^{n} {\sigma_j^x} $

$ H_{A} = \frac{1}{2}\sigma_z^1 + \frac{1}{2}\sigma_z^1\otimes\sigma_z^2 $

Ansatz for p=1

$ \left| \gamma_1,\beta_1 \right\rangle = e^{-i\beta_1H_B} e^{-i\gamma_1H_A} \left| ++ \right\rangle$

It is clear how a circuit for $ e^{-i\beta_1H_B} $ looks like, but I stuck in decomposing $ e^{-i\gamma_1H_A} $(more precisely it second term) into parametrised circuit acting on both qubits and depends on $\gamma_1$

Any help would be appreciated as well as any insight on multiple qubit decomposition.

Answer 1

Since $\sigma_z^1 = I \otimes Z$ and $\sigma_z^1 \otimes \sigma_z^2 = Z \otimes Z$ are commute with one another, that is $$ [\sigma_z^1 , \sigma_z^1 \otimes \sigma_z^2 ] = \sigma_z^1 \cdot \sigma_z^1 \otimes \sigma_z^2 - \sigma_z^1 \otimes \sigma_z^2 \cdot \sigma_z^1 = \boldsymbol{0} $$ we have that $$ e^{i\gamma_1 H_a} = e^{i \gamma \frac{1}{2}(\sigma_z^1 + \sigma_z^1 \otimes \sigma_z^2 ) } = e^{i \gamma \frac{1}{2}\sigma_z^1 } e^{i \gamma \frac{1}{2}\sigma_z^1 \otimes \sigma_z^2 } $$ and now note that $e^{i \gamma \frac{1}{2}\sigma_z^1 }$ has circuit construction as: (look here and here page 7 and 8)

and similarly, $ e^{i \gamma \frac{1}{2}\sigma_z^1 \otimes \sigma_z^2 } $ have the circuit construction as:

and put them together, we have the circuit construction for $e^{i \gamma \frac{1}{2}(\sigma_z^1 + \sigma_z^1 \otimes \sigma_z^2 ) }$ as: