Why does the phase of the eigenstate get kicked up to the ancilla qubit?

Question

I'm revisiting my knowledge on phase kickback, and I realize that there are many holes in my understanding. I've come across the definition that phase kickback is the phenomenon that occurs when you apply a controlled unitary where the target qubit is in an eigenstate of the unitary thus kicking the phase to the ancilla qubit So here's my question:

Why is it that when applying a controlled operation where the target qubit is an eigenstate, that the phase of that state gets kicked up to the ancilla qubit?

Answer 1

Here is a basic example of a two system that might help you to see this better. Suppose I have these two circuits:

Circuit 1: Which put the "Controlled qubit" in the state $|1\rangle$ and the "Target qubit" state in $H \big(X|0\rangle \big) = \dfrac{|0\rangle - |1\rangle}{\sqrt{2}} $. Note that this state, $|psi \rangle = \dfrac{|0\rangle - |1\rangle}{\sqrt{2}} $ is an eigenvector of the NOT gate $X = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}$ since $ X|\psi \rangle = X \bigg(\dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) = -1 \bigg(\dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) = -1|\psi \rangle $.

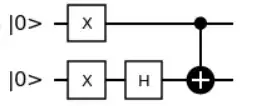
so here the state before the Controlled-NOT (CNOT) operation is $|1\rangle \bigg(\dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) = \dfrac{|10\rangle - |11\rangle}{\sqrt{2}}$.

hence

$$ CNOT \bigg( \dfrac{|10\rangle - |11\rangle}{\sqrt{2}} \bigg) = \dfrac{|11\rangle - |10\rangle}{\sqrt{2}} = - \bigg( \dfrac{|10\rangle - |11\rangle}{\sqrt{2}}\bigg) = - \bigg( |1\rangle \otimes \dfrac{ |0\rangle - |1\rangle}{\sqrt{2}} \bigg) $$

But as you know, the state $|\psi \rangle = - \bigg( |1\rangle \otimes \dfrac{ |0\rangle - |1\rangle}{\sqrt{2}} \bigg) $ and the state $|\phi \rangle = |1\rangle \otimes \dfrac{ |0\rangle - |1\rangle}{\sqrt{2}}$ are equivalent.

Circuit 2: Which put the "Controlled qubit" in the state $\dfrac{|0\rangle + |1\rangle}{\sqrt{2}}$, and "Target qubit" still in $\dfrac{|0\rangle - |1\rangle}{\sqrt{2}} $

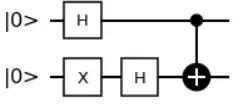
here the state before the Controlled-NOT (CNOT) operation is: $$\bigg(\dfrac{|0\rangle + |1\rangle}{\sqrt{2}} \bigg)\bigg(\dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) = \dfrac{|00\rangle - |01\rangle + |10\rangle - |11\rangle}{2}$$ Hence \begin{align} CNOT \bigg( \dfrac{|00\rangle - |01\rangle + |10\rangle - |11\rangle}{2} \bigg) &= \dfrac{|00\rangle - |01\rangle + |11\rangle - |10\rangle}{2}\\ &= \bigg( \dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) \otimes \bigg( \dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) \end{align}

From here we can see that the controlled qubit started in the state $\dfrac{|0\rangle + |1\rangle}{\sqrt{2}}$ but ended in the state $\dfrac{|0\rangle - |1\rangle}{\sqrt{2}}$. Thus, it has picked up the overall phase of the state: $ -1 \bigg(\dfrac{|0\rangle - |1\rangle}{\sqrt{2}} \bigg) $ as its relative phase.