How does the CX gate work?

Question

I have a silly question as I am an absolute beginner! So as described in Qiskit:

It performs the NOT operation (equivalent to applying an X gate) on the second qubit only when the first qubit is $|1\rangle$ and otherwise leaves it unchanged.

in the piece of the related program we have :

# Let's do an CX-gate on |00>
q = QuantumRegister(2)
qc = QuantumCircuit(q)
qc.cx(q[0],q[1])
qc.draw(output='mpl')

In my mind I need 2 inputs for a CX gate A & B as (q[0] and q[1]) so that it can control B and NOT A, and also a third qubit as an output. But here we have q[0] as an input and q[1] as an output apparently. Can anybody help me please to understand the logic?

Answer 1

When you apply the CNOT gate on the state $|00\rangle$ what you will get out is the state $|00\rangle$, as the CNOT gate logically do the following:

$CNOT|00\rangle = |00\rangle, \ \ \ CNOT|01\rangle = |01\rangle, \ \ \ CNOT|10\rangle = |11\rangle, \ \ \ CNOT|11\rangle = |10\rangle$

where $\bigg\{|0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} , |1\rangle\ = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \bigg\}$ represents the computational basis. Here we are taking the first qubit as the controlled qubit, and the second qubit as the target qubit. That is, if the first (Controlled) qubit is in the state $|1\rangle$ then you apply the $X$ (NOT) gate to the second (Target) qubit, otherwise you do nothing. Thus, in this setting the CNOT gate has matrix representation (in the computational basis) as:

\begin{equation}\label{CNOT matrix} CNOT = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \end{equation}

so that is what you implement when you run the circuit:

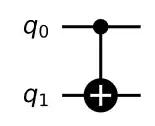
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
qreg_q = QuantumRegister(2, 'q')
creg_c = ClassicalRegister(2, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)
circuit.cx(qreg_q[0], qreg_q[1])
circuit.draw( 'mpl',style={'name': 'bw'}, plot_barriers= False, scale = 1)

as always, all state in quantum computer starts at the state $|00\cdots 0\rangle$. Hence, this means that for our circuit above $q_0 = |0\rangle$ and $q_1 = |0\rangle$, so the starting state is $|00\rangle = |0\rangle \otimes |0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\0 \\0 \end{pmatrix} $. Notice that

$$ CNOT|00\rangle = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\0 \\0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\0 \\0 \end{pmatrix} = |00\rangle $$

The input is the state of $|00\rangle$ and the output is also $|00\rangle$.

Note that: circuit.cx(qreg_q[0], qreg_q[1]) indicates that the controlled qubit is in the quantum register qreg_q[0] and it will act on the target qubit which is in the quantum register qreg_q[1]. And this can be changed. That is, you can make the qubit in the quantum register qreg_q[1] as your controlled qubit and the qubit in the quantum register qreg_q[0] as your target qubit by simply switch the 5th line of the code to: circuit.cx(qreg_q[1], qreg_q[0]). The circuit will look like:

---

If you instead input a different state, says $|10\rangle$ then the result would be different, it would be $|11\rangle$ in this case. That is, if you execute the circuit:

Note that the $X$ gate here is to put the qubit $q_0$ from the state $|0\rangle$ to $|1\rangle$. That is, we are making the input state $|10\rangle$. The output state now would be $|11\rangle$ as the controlled qubit is now in the state $|1\rangle$ so it will act on the target qubit by applying the $X$ (NOT) gate. If you run this on the simulator, you will see something like:

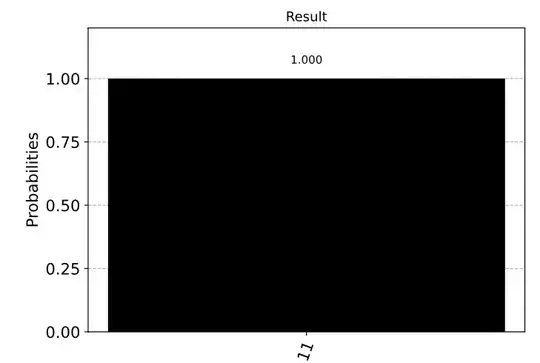
Here is the code to generate the following circuit and plot in Qiskit:

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, BasicAer, execute
from qiskit.visualization import plot_histogram
%matplotlib inline
qreg_q = QuantumRegister(2, 'q')
creg_c = ClassicalRegister(2, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)
circuit.x(qreg_q[0])
circuit.cx(qreg_q[0], qreg_q[1])
circuit.measure(qreg_q[0], creg_c[0])
circuit.measure(qreg_q[1], creg_c[1])
circuit.draw( 'mpl',style={'name': 'bw'}, plot_barriers= False, scale = 1)
backend = BasicAer.get_backend('statevector_simulator')
job = execute(circuit, backend, shots = 1)
plot_histogram(job.result().get_counts(), color='black', title="Result")

And you can work this out explicitly in matrix algebra as well:

$$ CNOT|10\rangle = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\1 \\0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\0 \\1 \end{pmatrix} = |11\rangle $$

Answer 2

The previous answer is rich enough and technically helpful. However, I would like to give an insight from different perspective. In quantum circuits, ALWAYS the number of inputs equals the number of outputs! The reason is that quantum circuit makes only transformation on the state of qubits and CANNOT clone (make copy of) them. Therefore, CX gate transform the target qubit depending on the control qubit which is remain unchanged.