0

I am trying to wrap my head around Qiskit Aqua Operators and I stumbled upon this:

My code

t=0.5
hamiltonian=get_hamiltonian(1,1) #a four 4 qubit hamiltonian (Transverse field Ising model)
evo_time=Parameter("t")

evo_op=(evo_time*hamiltonian).exp_i()
evo_op1 = evo_op @ (Zero^4)


trotter_op=PauliTrotterEvolution(trotter_mode=Suzuki(reps=10,order=1)).convert(evo_op1)
trotter_op_values=trotter_op.bind_parameters({evo_time: t})


circuit1=trotter_op_values.to_circuit()
backend=Aer.get_backend("qasm_simulator")
circuit1.measure_all()


counts1=execute(circuit1, backend=backend, shots=10024).result().get_counts()


for key in counts1.keys():
    counts1[key]=counts1[key]/10024


a=0


I had to instantiate again the trotter_op because trotter_op_values.to_circuit()


#didn't create a new circuit and instead, by having done circuit1.measure_all()


trotter_op was modified as well.


trotter_op=PauliTrotterEvolution(trotter_mode=Suzuki(reps=10,order=1)).convert(evo_op1)
trotter_op_values=trotter_op.bind_parameters({evo_time: t})
sampler=CircuitSampler(backend=Aer.get_backend("qasm_simulator"))
sampler.quantum_instance.shots=10024
results1=sampler.convert(trotter_op_values).primitive


#normalize the results from the circuitsampler
for key in results1.keys():
    a+=results1[key]
for key in results1.keys():
    results1[key]=results1[key]/a


assert counts1.keys()==results1.keys()


assert sum(counts1.values()) #check normalization
assert sum(results1.values()) #check normalization


for key in results1.keys():
    print("state: {} | Counts1: {} | Results1: {}".format(key,counts1[key], results1[key]))


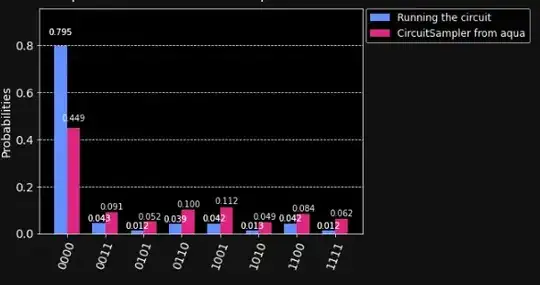
plot_histogram([counts1, results1], legend=["Running the circuit","CircuitSampler from aqua"])

What I expected Since the evo_op1 is just a CircuitStateFn whose initialization was the zero state for the 4 qubits then, passing this into CircuitSampler the CircuitStateFn would be replaced by a DictStateFn whose amplitudes would be the same as measuring all 4 qubits in the trotterization circuit with a zero state initialization (my circuit1).

What I got The histograms never match, for any value of t except t=0. However, there is always a clear similarity between the plots (for small t the probability for 0000 is always the biggest for example and all other states have similiar probabilities, but never exactly equal)

enter image description here

What am I missing? Was it a bad interpretation of the Operator Flow?

glS
  • 24,708
  • 5
  • 34
  • 108
Bidon
  • 818
  • 5
  • 15

1 Answers1

1

Well, you are right. After CircuitSampler you are getting a DictStateFn with phase information lost (see the docs) in the amplitudes and you have to take the square of them for your histogram plot (not normalize).

Besides that, just keep in mind that the number of shots are not stored in the QuantumInstance of CircuitSampler (in the way you are setting them). You should rather do

qinstance = QuantumInstance(backend, shots=10024)
sampler = CircuitSampler(qinstance)
tsgeorgios
  • 1,416
  • 1
  • 5
  • 5
  • Thank you! That solved it perfectly. If I may, I added a question a few hours ago about time evolution of a quantum state (https://quantumcomputing.stackexchange.com/questions/13884/how-to-perform-a-time-evolution-of-a-quantum-state-with-qiskit-aqua). Would you say that this is an efficient way to evolve a quantum state in Aqua? Or is there a better way? – Bidon Sep 23 '20 at 11:08