Is it possible (in theory) to convert any problem that can be solved on a quantum computer into an arrangement of slits carved into a piece of metal foil, and then to run the program by shining light on the foil and observing the pattern of light that it produces?
It seems to me that this should be possible, just as any program on a conventional computer can be transformed into a boolean circuit (in theory).
If it were as easy as cutting slits into metal foil, or even doing photolithography at the sub-10nm regime, then it would have been done by now, but that might not be a satisfactory answer. It's a good question and should not be dismissed.
The question is similar to "what is stopping us from achieving a computational speedup by running Shor's algorithm by merely cutting a bunch of slits into a metal foil, and looking at the interference patterns when light is shown through?" .
Indeed, Shor has referred to Shor's algorithm as a "computational interferometer." For example, one thing that quantum computers can do, and that diffraction gratings can do, is perform Fourier transforms on large data sets.
But diffraction gratings don't have much in the way of adaptive control, and you have to spend exponential resources before-hand in order to leverage the constructive and destructive interference of the photons.
For example, you could cut slits in your foil in a manner where the spacing is $a^x\bmod N$. Shining light through such a diffraction grating, even a single photon of light, will perform the quantum Fourier transform.
However, in this case you had to cut your diffraction grating a-priori into $a^x\bmod N$; that is, you had to perform an exponential number of cuts in the first place.
It's not clear how such non-adaptivity is still powerful enough to solve Shor's algorithm, or whether you would always need to pre-cut your grating with an exponential number of cuts in the first place.
Indeed, the very procedure in the questions was proposed by Clauser and Dowling back in '96, in a PRA paper titled "Factoring integers with Young's N-slit interferometer." They use such an experiment to factor $143$ into $11\times 13$ as below.
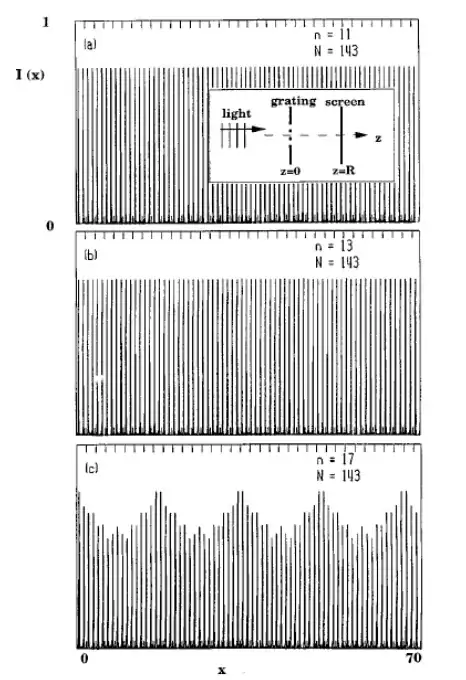
They estimate that, with the lithography of 1994, they could factor four-to-five digit numbers (I guess with current photolithography 30 years on we could maybe factor numbers up to a billion or so).
But of note Clauser and Dowling still emphasize that there'd be exponential scaling of resources if using only coherence and interference (and not using entanglement). To factor cryptologically significant numbers, one would have to tighten the spacing further and/or ramp up the laser power exponentially as well.
As far as I understand your scheme, it is equivalent/can be modelled as a multiport interferometer. Think a generalisation of a (not necessarily balanced) beamsplitter to many modes.
If the input is classical (i.e. coherent light) then the output of an interferometer can be simulated efficiently classically, meaning that this is not useful for quantum computation. The same goes when the input is a single photon.
Things get more interesting when using as input multiple single photons on different inputs modes. Then we know that this setup cannot be simulated efficiently with a classical device. However, as far as I know, it is not known whether it is possible to implement "useful" quantum algorithms with this type of device.
I think the simplest way to think about this (inspired by Mark S's answer) is simply to acknowledge that with a series of slits, you'd get the correct interference pattern with a single photon. But to do an $n$-qubit computation, you need a Hilbert space of dimension $2^n$, which you're encoding in a path. In other words, you need $2^n$ possible paths. So, immediately, you need exponentially scaling resources, meaning that you cannot get a speed-up over classical.
