How do I find the matrix and circuit equivalent to this transformation?

Question

First I would like to find the matrix corresponding to the transformation and then implement it with rotational gates. How can I do it?

Answer 1

The matrix for $\sigma_z \otimes \sigma_z$:

$$\sigma_z \otimes \sigma_z = \begin{pmatrix} 1&0&0&0 \\ 0&-1&0&0 \\ 0&0&-1&0 \\ 0&0&0&1 \\ \end{pmatrix}$$

The matrix for $e^{-i\sigma_z \otimes \sigma_z t}$, where $t$ is some parameter:

$$e^{-i\sigma_z \otimes \sigma_z t} = \begin{pmatrix} e^{-i t}&0&0&0 \\ 0&e^{i t}&0&0 \\ 0&0&e^{i t}&0 \\ 0&0&0&e^{-i t} \end{pmatrix}$$

The circuit for this operator (like described in this paper):

                                                       

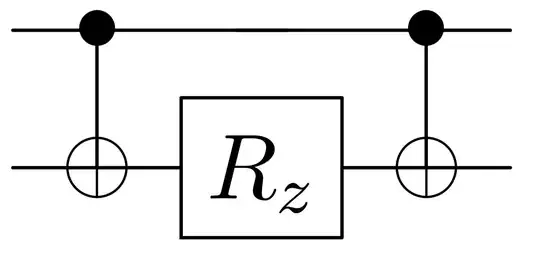
where $R_z$'s argument is $2t$. An explicit explanation about why this circuit implements the operator mentioned above can be found here. Or can be seen after doing matrix multiplication for the gates presented in the circuit:

$$ \text{CNOT} \cdot I \otimes R_z(2t) \cdot \text{CNOT} = \\ = \begin{pmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \end{pmatrix} \begin{pmatrix} e^{-i t}&0&0&0 \\ 0&e^{i t}&0&0 \\ 0&0&e^{-i t}&0 \\ 0&0&0&e^{i t} \end{pmatrix} \begin{pmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \end{pmatrix} = e^{-i\sigma_z \otimes \sigma_z t} $$