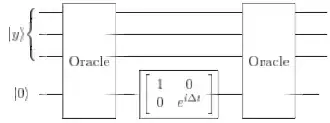
Firstly let's use Taylor series (I will write $t$ instead of $\Delta t$):
\begin{equation}
e^{-i |x \rangle \langle x | t} = I + (-i |x \rangle \langle x | t) + \frac{(-i |x \rangle \langle x | t)^2}{2!} + \frac{(-i |x \rangle \langle x | t)^3}{3!} ... =
\\
= \left( I + (-i t) + \frac{(-i t)^2}{2!} + \frac{(-i t)^3}{3!} ... \right) |x \rangle \langle x | + I(1 - |x \rangle \langle x|) =
\\
= I + (e^{-it} - 1) |x \rangle \langle x |
\end{equation}
So the circuit should implement the operator $I + (e^{-it} - 1) |x \rangle \langle x |$.
Now what does the Oracle (from the M. Nielsen and I. Chuang textbook):
$$|x\rangle |q\rangle \xrightarrow[]{\text{O}} |x\rangle |q \oplus f(x)\rangle$$
So, if $|q\rangle = |0\rangle$ as mentioned in the circuit, and note that $f(x) = 1$ only if $x$ is a solution, otherwise $f(x) = 0$. The operator that corresponds to the Oracle (here I am assuming (also assumed in the book) that we have only one solution):
$$O = \sum_{y \ne x} |y\rangle \langle y| I + |x\rangle \langle x| X = II + |x\rangle \langle x| (X - I) $$
Let's see what the combined action looks like (the phase gate is denoted as $P$ and $II \equiv I$):
\begin{equation}
O \: I \cdot P \: O = \left[ I + |x\rangle \langle x| (X - I) \right] I \cdot P \left[ I + |x\rangle \langle x| (X - I) \right]=
\\
= I \cdot P + |x\rangle \langle x| P(X - I) + |x\rangle \langle x| (X - I) P +|x\rangle \langle x| (X - I) P (X - I) =
\\ = I \cdot P - |x\rangle \langle x| P + e^{it}|x\rangle \langle x| P^{\dagger}
\end{equation}
because $XPX = e^{it}P^{\dagger}$. Let's take into account that the ancillary qubit starts in the $|0 \rangle$ state, then the combined operator will look like (by omitting the $P$ and $P^{\dagger}$ applyied on the ancillary qubit, because they do noting on the $|0 \rangle$ state and thus the ancillary qubit is "out of the game"):
\begin{equation}
I - |x\rangle \langle x| + e^{it}|x\rangle \langle x| = I + (e^{it} - I)|x\rangle \langle x|
\end{equation}
How one can see there is the inconsistency of $-$ sign in the phase like in this answer to the related question, because, maybe I did a mistake, or perhaps, there is a typo in the book. Now let's draw an example when $|x\rangle = |0101\rangle$ (I will show the simplest example: the implementations can be different depending on what we want to find with Grover, but one thing should be the same: in all cases $|0101\rangle$ should be a solution):
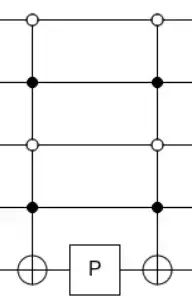
where the leftmost qubit in $|0101\rangle$ corresponds to the first wire. The circuit is drawn with quirk. The way of implementing the Oracle shown above more explicitly can be understood from this answer about black and white dots in the circuit and this answer about multi-controlled gates.