The answer to my question is given here. The solution from the provided paper is extremely efficient (for it requires $O(n^2 / \log n)$ CNOTs instead of the naïve $O(n^2)$ estimate), and is somewhat nontrivial to implement.
An easy-to-implement solution with $O(n^2)$ CNOTs can be, however, obtained in just a few lines. First of all, one has to perform the LU-decomposition of the desired matrix $M$. This can be done as follows:
P, L, U = scipy.linalg.lu(M)
L = np.mod(L, 2)
U = np.mod(U, 2)
Luckily, for an invertible matrix $M$, the resulting $P,L,U$ matrices will contain binary entries. Here $P$ is a permutation matrix, and $L$ and $U$ are the lower- and upper-triangular matrices, whose product is the original matrix, $M = P \ L \ U$.
Permutations $P$ can be implemented using SWAPs. Multiplication by a triangular matrix is also quite straightforward, and is done using CNOTs starting from the most occupied row. In other words, for $U$ one should start from the first row: once the first qubit is calculated, it is never used in the following calculation, and so on. If you, say, wanted to transform qubits according to
$$
M
\begin{pmatrix}
q_0 \\ q_1 \\ q_2
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 & 1 \\
0 & 1 & 1 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
q_0 \\ q_1 \\ q_2
\end{pmatrix} \ ,
$$
the circuit would look like
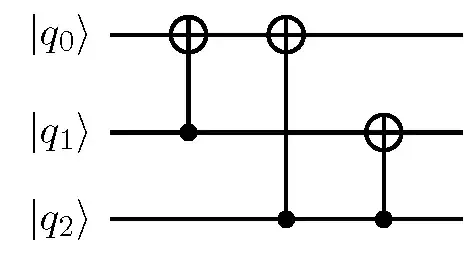
A typical scenario in which one may need to implement such a matrix transformation on qubit registers arises in quantum simulation. Namely, in order to encode a state of a fermionic system using the Bravyi-Kitaev encoding, one needs to perform a matrix transformation of the original qubit registers (which can equivalently be thought of as being Jordan-Wigner encoded).
Interestingly enough, the Bravyi-Kitaev encoder matrix is lower-triangular from the very beginning [1], so in this particular case there is no need to perform the LU-decomposition.
