This work (which I'm a co-author) discusses the properties that different forms of money have. The paper discusses cryptocurrencies such as Bitcoin, and public quantum money.
The following figure is taken from there, where the two relevant columns are highlighted: 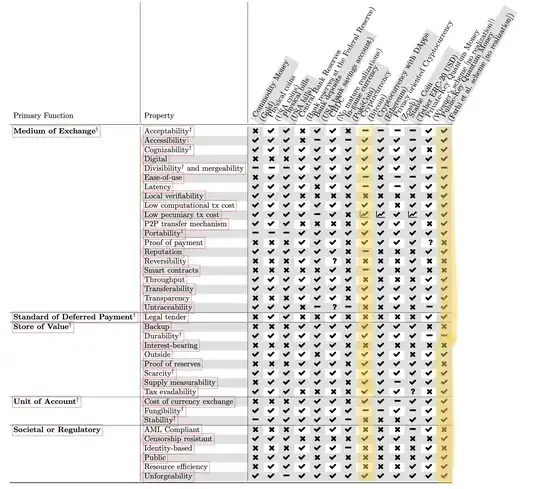
The advantages, some of which were not mentioned by others, is that public quantum money is locally verifiable (meaning, unlike Bitcoin, you don't need to be connected to the internet), there are no transaction costs, low latency, has an unbounded throughput (e.g., Bitcoin can only support <10 transactions per second, globally), provides better privacy guarantees (untraceable, at least to some extent), more fungible than Bitcoin and other cryptocurrencies which are not privacy oriented, and is energetically much more efficient (as it doesn not reuqire proof-of-work).
Public quantum money could be issued by a cenral bank (similarly to cash), and in this case it would enjoy other benefits such as of it being legal tender, stable and have a better reputation.
The drawbacks of public quantum money are: it is not divisible or mergeable, does not allow proof-of-payment nor proof-of-reserves, does not provide smart contracts functionalities, and it can't be backed-up.
There are some more advnaced primitives, such as quantum lighting and one-shot signatures, which can be used to eliminate some of the drawbacks mentioned above: see here and here. Unfortunately, we currently don't have constructions which are provably secure in the plain model for these primitives. I consider constructing these primitives an important open problem.
