6

I'd like to understand a graph theoretic property in terms of group theory. I have some boring graphs, and some neat graphs, all created from groups, but I don't know how to tell a boring group from a neat group.

Is there a group-theoretic formulation of the existence of a 4-cycle in the coset graph of a completion of the amalgam 2←1→2×2?

Background: This just defines a coset geometry or coset graph for an amalgam.

Given a group G and two subgroups H, K, define a simple bipartite graph Γ whose green vertices are the cosets of H and the red vertices are the cosets of K, and whose edges are between those cosets that have non-empty intersection.

In terms of graph theory, this gives a connected bi-regular graph where the green vertices have degree $[H:H\cap K]$ and the red vertices have degree $[K:H\cap K]$. G acts as automorphisms of the graph, with H the stabilizer of a green vertex, K the stabilizer of a red vertex, and H ∩ K the stabilizer of a directed edge.

The special case and question: When $[K:H\cap K]=2$ the graph Γ is a line graph of a multi-graph Γ′ found by contracting one edge per red vertex.

When does Γ′ have multiple edges? Equivalently, when does Γ have a cycle of length 4?

I am interested in a fairly silly case: K has order 2, H is the Klein 4-group, H ∩ K = 1, and G is generated by H and K. In short: G is a completion of the amalgam 2←1→2×2. The bipartite graph must have two commuting involutive automorphisms fixing a green vertex, an involutive automorphism fixing a red vertex, and the subgroup generated by those must act transitively on the red and green vertices. An earlier question asked about the simply connected covering space of these graphs.

The red vertices all have degree 2, and I guess it is well-known that topologically these are very dull: they just divide an edge into two edges without changing any real connectivity. In other words, to find the simply connected covering space of the free product, we could have completely ignored the subgroup of order 2, and then we get a standard example of the tree corresponding to the Klein 4-group (with red vertices dividing all the edges).

The finite quotients are fairly pretty, but some of them are both irritating and boring: the red vertices are necessary to distinguish two edges between the same green vertices (that is, the graph Γ has a cycle of length 4, and so the graph Γ′ has a double edge). I want to know what it is about the group G that results in these cycles of length 4 in Γ and these double edges in Γ′.

Illustrative illustrations: Here are some pictures to show the difference between the boring ones where Γ′ has multiple edges, and the neat ones where it does not. The picture of the graph Γ′ is formed from the picture of the graph Γ by ignoring the red dots.

There is a "boring" graph for any given number of green nodes: Arrange n green nodes evenly on a circle, and then make the inscribed regular polygon. Divide each edge (both the curvey ones making the circumference of the circle, and the straight ones making the inscribed polygon) in half using a red node (a total of $2n$ red nodes). One can (1) switch the inner circle with outer, (2) reflect the whole thing about a diameter through a green vertex, and (3) reflect the whole thing about a diameter going through a red vertex, giving the three required automorphisms. Basic facts about dihedral groups show that the group generated by these is bi-transitive.

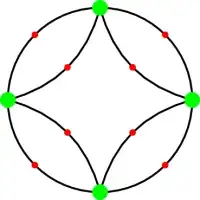
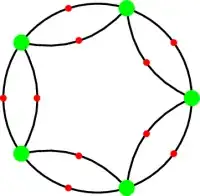
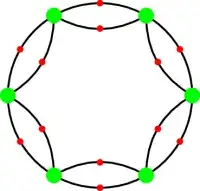
However, there are a few neat ones, such as two triangles inscribed in a circle:

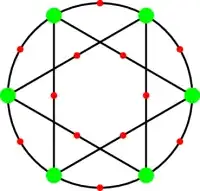
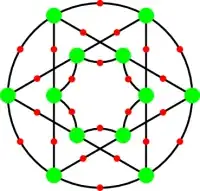
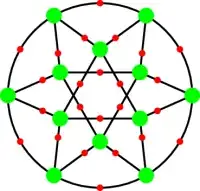
These were found by looking at quotients of the universal cover with low degree permutation representations.

It would be nice if the answer also helped answer the question:

Which n are such that there is a neat graph on n green vertices (for 2←1→2×2)?

Glorfindel
  • 3,955
Jack Schmidt
  • 55,589

1 Answers1

2

Short cycles are very easy to understand, since G acts edge transitively, and the edges coming out the vertices H and K are easy to understand. If H is small, we can phrase the 4-cycle condition somewhat nicely in terms of fusion. If K is an abelian Sylow 2-subgroup, then we can relate this the centralizer of the involution in H.

Lemma: Every trail of length 3 in the coset graph of G on H, K is conjugate to the trail: $\newcommand{\edge}[1]{~\xrightarrow{#1}~}$ $$kH \edge{k} K \edge{1} H \edge{h} hK$$ for some elements h in H and k in K neither contained in H ∩ K.

Proof: Since G acts edge-transitively on the coset graph, we can assume the middle edge is $K\edge{1} H$. If the left-most edge is labelled by g, then g is contained in the intersection of the left vertex and K, but in particular, g is in K. Since the edges are distinct, g cannot be contained in H ∩ K. $\square$

Proposition: If H = { 1, h }, then the coset graph of G on H and K has a 4-cycle if and only if there is some non-identity element k of K such that $k^h$ is also in K.

Proof: If $k$ and $k^h$ are in K, then $kH \edge{k} K \edge{1} H \edge{h} hK \edge{h k^h = kh} kH$ is a 4-cycle. Conversely, if the coset graph of G has a 4-cycle, then WLOG the 4-cycle is: $$kH \edge{k} K \edge{1} H \edge{h} hK \edge{x} kH$$ where $x = hk_1 = kh_1$ is an element of both hK and kH. Since hK ≠ K, h1 is not contained in H ∩ K, but H is so small that forces h1 = h, and so $k_1 = k^h$ is also in K. $\square$

Proposition: If H is order 2, and K is an Abelian Sylow 2-subgroup of G, then the coset graph of G on H, K has a 4-cycle if and only if the centralizer of H in K is nontrivial and H ∩ K = 1.

Proof: If H ∩ K ≠ 1, then it is equal to H, and H is a leaf, making the graph a disjoint union of edges (and so having no 4-cycle). Since K is an Abelian sylow, two elements of K are conjugate by h if and only if they are equal (and thus centralize h). $\square$

This helps understand the graphs with Γ′ having an odd number of vertices (so that K is an abelian Sylow 2-subgroup). Then K cannot centralize H, since H is not contained in K, but certainly centralizes itself and K is a maximal 2-group. Hence we get a quotient of $$\langle x,y,z : x^2, y^2, z^2, yx=xy, zy=yz \rangle$$

Such a group appears to be dihedral if it has order 4 mod 8, though I'm not quite sure why.

Community
  • 1
Jack Schmidt
  • 55,589