5

Let $f: [0, \infty) \longrightarrow \mathbb{R}$, where $\lim_{x \to \infty}f(x)$ exist, show that $\lim_{x \to \infty}f′(x)=0$

This fact is clearly intuitive to me but I could not write a rigorous demonstration of this.

copper.hat
  • 172,524
Jhon Jairo
  • 1,031

3 Answers3

7

The fact is false. Here is a counterexample: 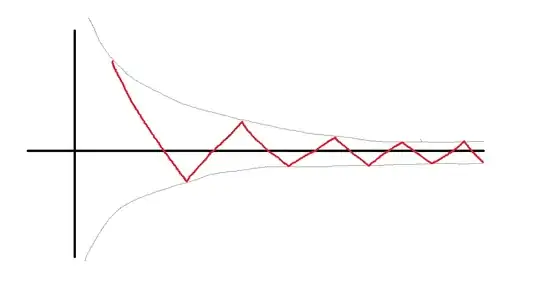enter image description here

You can smooth the corners so that $f'(x)$ is defined everywhere, but alternates between $+1$ and $-1$, so has no limit as $x\to \infty$. Meanwhile, $f(x)$ is squeezed between curves that approach zero, so $f(x)\to 0$.

vadim123
  • 82,796
  • It's not true, but would it be true for non-oscillating functions? And if so, how would we then prove it? – Axoren Oct 27 '14 at 03:23
  • 1
    What does "non-oscillating" mean? You can make the red curve hug the top asymptote, then go at slope $-1$ to hug the bottom one, then up again. You can make this happen in a non-periodic way if you like, even at random, and the counterexample still stands. – vadim123 Oct 27 '14 at 03:28
  • @Axoren, it's not even true for monotonic functions. – Kaj Hansen Oct 27 '14 at 03:31
  • @KajHansen Could you give an example? It's late and I can't think of a monotonic function that it breaks for? – Axoren Oct 27 '14 at 03:41
  • but in the peaks of the function the derivative is not defined , if the derivative is defined in the interval $(0, \infty)$ the result is true ? or which condition is necessary for this? – Jhon Jairo Oct 27 '14 at 03:42
  • You can smooth the corners so that $f'(x)$ is defined everywhere; if you want an explicit function see @KajHansen's solution which is pretty much the red curve. – vadim123 Oct 27 '14 at 03:43
  • 1
    @user67427, consider the image attached. We have a "step" that occurs at constant intervals, and that step gets smaller and smaller each time. However, at each step the derivative is $>>0$. From here, we can smooth out the steps to make the function differentiable. The resulting function is monotonic, limits to zero, and yet the derivative does not limit to zero. http://i.imgur.com/ePn2xxp.png – Kaj Hansen Oct 27 '14 at 04:15
6

This seems intuitive at first glance, but it's not true. Consider the following function:

$$f(x) = \frac{\sin(x^2)}{x+1}$$

To make this easier to see, consider instead the corresponding example for $g:(0, \infty) \rightarrow \mathbb{R}$:

$$g(x) = \frac{\sin(x^2)}{x}$$

And computing a derivative:

$$g'(x) = 2\cos(x^2) - \frac{\sin(x^2)}{x^2}$$

Certainly, $\displaystyle \lim_{x \rightarrow \infty} g(x) = 0$, but $\displaystyle \lim_{x \rightarrow \infty} g'(x)$ does not exist.

The above example was built out of this one so that it will be defined at $x = 0$.

Kaj Hansen
  • 33,011
1

First I think the necessary assumption is $f'(x)$ exist for all $x\in[0,\infty)$ otherwise the conterexamples are given in other answers. Here is another one, $f(x)=\frac{1}{x}$ when $x$ is rational and $0$ when $x$ is irrational, the function is discontinuous everywhere(therefore no derivative exist) but satisfies your criteria.

Assume $f'(x)$ exist everywhere, let $lim_{x\rightarrow\infty}f'(x)=a>0$. We can prove $lim_{x\rightarrow\infty}f(x)=\infty$, for given $\epsilon=\frac{a}{2}>0$, we can find $\delta>0$ such that $x>\delta$ implies $f'(x)>a-\epsilon=\frac{a}{2}>0$. We know continuous function($f'$ exist so f continuous) is integrable and we have $$f(\delta+\gamma)=f(\delta)+\int_{\delta}^{\delta+\gamma}f'(x)dx>f(\delta)+\frac{a\gamma}{2}$$ for any $\gamma>0$. This implies $f(x)$ can be arbitrary large for large enough $x$, and that's what $lim_{x\rightarrow\infty}f(x)=\infty$ means.

The prove of the cases $a<0$ or $a=\pm\infty$ are similar.