How to evaluate $ \int_{0}^{1} x^{x^{x^{x^…}}} dx $

Question

Inspired by the fact that $\int_0^1 \frac{1}{x^x}=\sum_{k=1}^\infty \frac{1}{k^k}$ I asked myself wether it is possible to evaluate the following integral: $$ \int_{0}^{1} x^{x^{x^{x^…}}} dx $$ In a similar way. Any help is highly appreciated.

Answer 1

This is not a proper answer. But an approach that explores the recursive aspects of the problem that I imagine lead to the expected solution. Define the functions $\varphi: (0,+\infty)\to [0,+\infty]$ and $\varphi_n: (0,+\infty)\to [0,+\infty]$ by

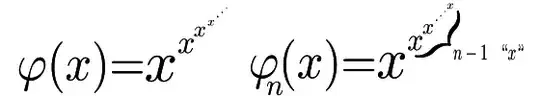
More precisely these functions are defined by recursion: $$ \varphi_{n}(x)= \left\{ \begin{array}{rcl} x, & \mbox{ if } & n=1\\ x^{\varphi_{n-1}(x)}, & \mbox{ if } & n> 1 \end{array} \right. \quad \mathrm{ and } \quad \varphi(x)=\lim_{n\to \infty}\varphi_n(x) $$ if the limit exists. In the case of $x$ between $0$ and $1$ such limit exists, i.e. for all $\frac{1}{2}>\epsilon>0$ and $x\in[\epsilon, 1]$ the limit $\varphi(x)=\lim_{n\to\infty}\varphi_n(x)<\infty$ exists. Taking care with convergence limits, $$ \int_0^1\varphi(x)\mathrm{d} x = \lim_{\epsilon\to 0}\int_\epsilon^{1}\lim_{n\to\infty}\varphi_n(x)\mathrm{d} x $$ By the Lebesgue's Dominated Convergence Theorem ( $|\varphi_n(x)|\leq 1$ for all $x\in[\epsilon, 1]$ for all $\epsilon >0$). $$ \int_0^1\varphi(x)\mathrm{d} x= \lim_{\epsilon\to 0}\lim_{n\to\infty}\int_\epsilon^{1}\varphi_n(x)\mathrm{d} x $$ Now let's get a more tractable procedure to approximate the integral $ \int_\epsilon^{1}\varphi_n(x)\mathrm{d} x \quad \mbox{ for all } n. $ Note that \begin{align} \log\varphi_{n}(x)=& \varphi_{n-1}(x) \log x \\ \log^{2}\varphi_{n}(x)=& \varphi_{n-2}(x) (\log x )^2\\ \log^{3}\varphi_{n}(x)=& \varphi_{n-3}(x) (\log x )^3\\ \vdots\;& \hspace{2cm}\vdots \\ \log^{k}\varphi_{n}(x)=& \varphi_{n-k}(x) (\log x )^k\\ \vdots\;& \hspace{2cm}\vdots \\ \log^{n-2}\varphi_{n}(x)=& \varphi_{2}(x) (\log x )^{n-2}\\ \log^{n-1}\varphi_{n}(x)=& \varphi_{1}(x) (\log x )^{n-1}\\ \end{align} Then $\varphi_n(x)=\exp^{n-1}\left(x \cdot (\log x )^{n-1}\right)$ \begin{align} \int_0^{1}\varphi (x)\mathrm{d} x & = \lim_{\epsilon\to 0}\int_{\epsilon}^{1}\lim_{n\to \infty}\varphi_n(x)\mathrm{d}x \\ & = \lim_{\epsilon\to 0}\int_{\epsilon}^{1}\lim_{n\to \infty}\exp^{n-1}\left(x\cdot (\log x)^{n-1}\right)\mathrm{d}x \\ & = \lim_{\epsilon\to 0}\lim_{n\to \infty}\int_{\epsilon}^{1}\exp^{n-1}\left(x\cdot (\log x)^{n-1}\right)\mathrm{d}x \\ & = \lim_{n\to \infty}\lim_{\epsilon\to 0}\int_{\epsilon}^{1}\exp^{n-1}\left(x\cdot (\log x)^{n-1}\right)\mathrm{d}x \end{align}