They say that the right and left limits do not approach the same value hence it does not satisfy the definition of derivative. But what does it mean verbally in terms of rate of change?
-
2At the origin, the absolute value function "bends" - it goes from decreasing with a slope of -1 to increasing with a slope of 1. – Asier Calbet Oct 26 '14 at 09:25
-
5Can you draw a tangent line to the graph of the absolute value function at $x=0$? – Ittay Weiss Oct 26 '14 at 09:30
-
1at $x=0$ The function which is travelling at slope $-1$ Suddenly starts travelling at $+1$... Intuitively it is same as a car travelling at $50 Kmph$ at no point of time travelling at $100 Kmph$ which is not possible... – Praveen Kumaran P Sep 01 '23 at 05:56
1 Answers
There are 2 ways to understand your question, one is asking for a proof, the other is asking for intuitive reasoning, I will answer both here.
Proof that $|x|$ is not differentiable at $x=0$
We are trying to find
$$\lim_{h\to0}\frac{f(0+h)-f(0)}{h}\quad\text{where }f(x)=|x|$$ $$\lim_{h\to0}\frac{|0+h|-|0|}{h}$$ $$=\lim_{h\to0}\frac{|h|}{h}$$ Let's find the right limit $$=\lim_{h\to0^+}\frac{|h|}{h}$$ Since $h>0$ $$=\lim_{h\to0^+}\frac{h}{h}=1$$ Let's find the left limit $$=\lim_{h\to0^-}\frac{|h|}{h}$$ Since $h<0$ $$=\lim_{h\to0^-}\frac{-h}{h}=-1$$
If the left and right limits are not the same, the limit does not exist.
Intuitive reasoning
What does the derivative represent? The slope of the tangent line. Looking at different values of the absolute value function in some plots:
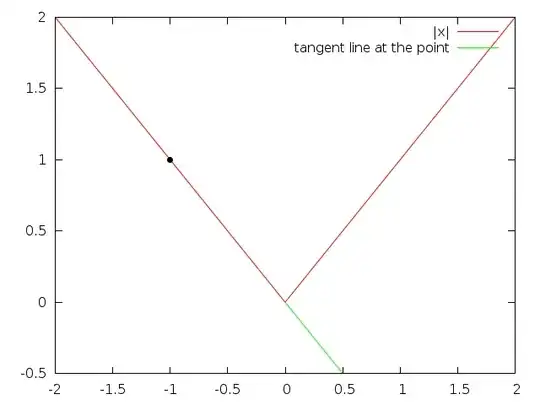
Note that the tangent line is below the actual line for the absolute value function.
The problem with the derivative at $x=0$ is that it changes abrubtly, and derivatives don't like that. Compare to the same plot but with $x^2$
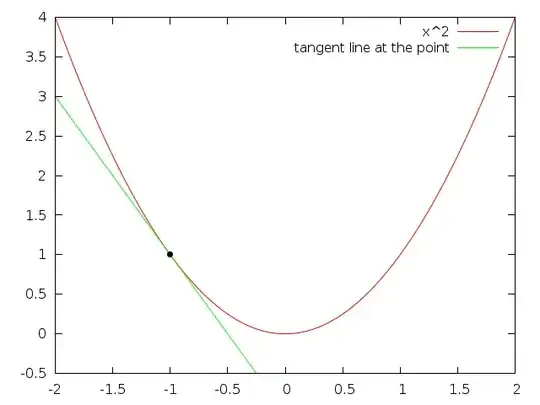
The difference is clear, the tangent line smoothly changes when approaching $x=0$ instead of the abrubt change from one line to another. This is why the derivative does not exist at $x=0$ for $|x|$.
Another way to think about derivatives is as “the slope of the line you get, when you zoom in really far”. If you zoom in on $x^2$ it'll look a lot like a straight line, but if you zoom in on $|x|$, it will never look like a straight line. If a function is differentiable, it will look like a straight line when you zoom in far enough.
- 7,853
-
9@Amzoti The individual frames were made by gnuplot. Then I used imagemagick to convert them into a gif. – Alice Ryhl Oct 26 '14 at 13:27
-
1That image program looks excellent, I will take it for a spin. Thanks for the reference! +1 – Amzoti Oct 26 '14 at 13:33
-
One should be wary of what is claimed to be wrong with the abrupt change. A function can be differentiable while having a discontinuous derivative. – Jonas Meyer Oct 29 '14 at 21:57
-
-
2Sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere differentiable, but with derivative discontinuous at $0$. I'd suggest googling discontinuous derivative for more info. If you want to see what's going on in your example, you can look into why a derivative can't have a jump discontinuity. That is, if the derivative exists, and the limit of the derivative on both sides of the point exist, then these all must be equal. But the limit need not exist. – Jonas Meyer Oct 29 '14 at 22:00
-
@JonasMeyer However that function dosen't do any abrubt cuts like $|x|$ does, both sides just kinda swirl into the point 0 in smaller and smaller swirls – Alice Ryhl Oct 29 '14 at 22:11
-
@KristofferRyhl: It sounds like you're on the same topic as the last three sentences of my last comment. – Jonas Meyer Oct 29 '14 at 22:14
-
-
-