Rule. The square of a sum is equal to the sum of the squares of all the summands plus the sum of all the double products of the summands in twos:
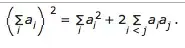
But I do not know how to calculate the square of summation of products >>
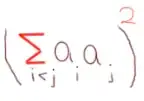
Rule. The square of a sum is equal to the sum of the squares of all the summands plus the sum of all the double products of the summands in twos:
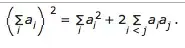
But I do not know how to calculate the square of summation of products >>
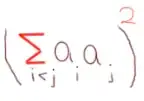
You want to show that $$\displaystyle \left(\sum_{i=1}^{j}a_i\right)^2=\sum_{i=1}^{j}a_i^2+2\sum_{i<j}a_i a_j$$
Proof by induction
Base step - $j=1$, so $\displaystyle a_1^2=a_1^2$, which is true.
Inductive step - assume that the claim holds for $j=k$ and prove it holds for $j=k+1$.
By assuming that the claim holds for $j=k$ we can write that $\displaystyle \left(\sum_{i=1}^{k}a_i\right)^2=\sum_{i=1}^{k}a_i^2+2\sum_{i<k}a_i a_k$.
We want to show that $\displaystyle \left(\sum_{i=1}^{k+1}a_i\right)^2=\sum_{i=1}^{k+1}a_i^2+2\sum_{i<k+1}a_i a_{k+1}$.
Splitting the sum we get $$\left(\sum_{i=1}^{k}a_i+a_{k+1}\right)^2=\sum_{i=1}^{k}a_i^2+a_{k+1}^2+2\sum_{i<k}a_ia_k+2a_ka_{k+1}$$ Using the assumption for $k=2\rightarrow\displaystyle \left(\sum_{i=1}^{2}a_i\right)^2=a_1^2+a_2^2+2a_1a_2$ we get $$\left(\sum_{i=1}^{k}a_i+a_{k+1}\right)^2=\left(\sum_{i=1}^{k}a_i\right)^2+a_{k+1}^2+2a_{k+1}\sum_{i=1}^ka_i$$ By assumption $\displaystyle \left(\sum_{i=1}^{k}a_i\right)^2=\sum_{i=1}^{k}a_i^2+2\sum_{i<k}a_i a_k$, thus$$\left(\sum_{i=1}^{k+1}a_i\right)^2=\sum_{i=1}^{k}a_i^2+a_{k+1}^2+2\sum_{i<k}a_i a_k+2a_{k+1}\sum_{i=1}^{k}a_i$$ Eventually, $$\left(\sum_{i=1}^{k+1}a_i\right)^2=\sum_{i=1}^{k+1}a_i^2+2\sum_{i<k+1}a_ia_{k+1}$$