4

I'm learning about inner product spaces and I am able to prove it within an inner product space. Is this a theorem or an axiom in euclidean geometry?(note: not the geometry of Descartes)

Hanul Jeon
  • 27,376
shooting-squirrel
  • 1,081
  • 7
  • 23
  • 2
    It can be easily proved by Pythagorean theorem, and I am sure it is not one of the five axioms in $Elements$. So I would say it is a theorem. – NECing Oct 23 '14 at 02:40

1 Answers1

3

As pointed out in the comments, it is definitely a theorem. Here is the shortest proof I could think of.

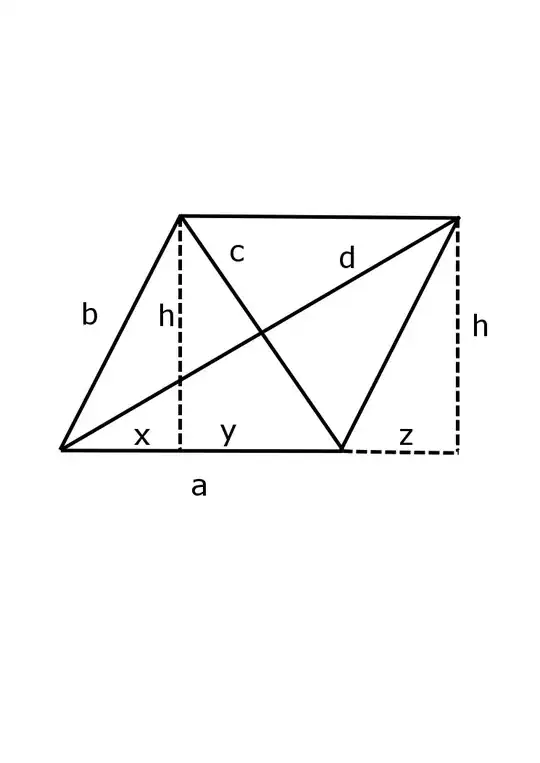
If the parallelogram is a rectangle, then the equality holds. Therefore we can assume the parallelogram has an acute angle. Label the parallelogram as in the figure, where the lines of length $h$ are perpendicular to the top and bottom. Also, notice that the right triangles with sides labeled x,h, and b and z,h,b are congruent so $x=z$. From the pythagorean theorem we get the following equalities:

$b^2=x^2+h^2$, $c^2=h^2+y^2$, $d^2=(2x+y)^2+h^2$, and so

$c^2+d^2= 4x^2+4xy+y^2+h^2+h^2+y^2=2(x^2+h^2)+2(x+y)^2=2b^2+2a^2$, as desired.

The labeled parallelogram

Neil Hoffman
  • 231