0

Figure

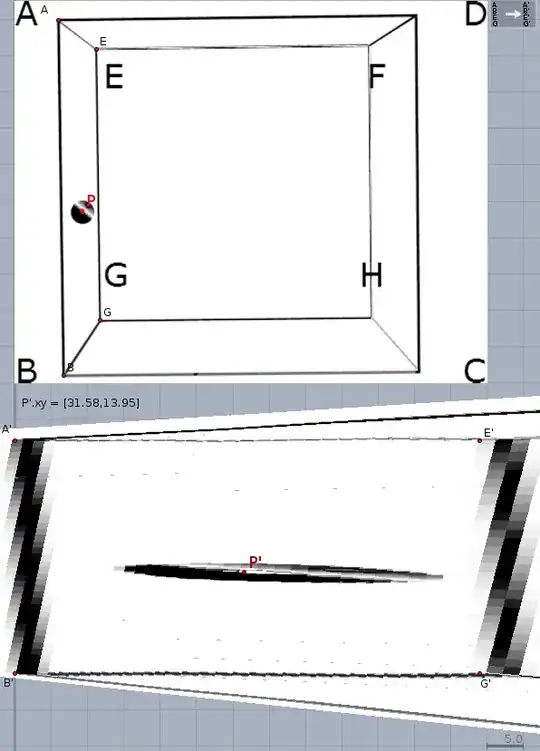
I have a box, with corners $A$ through $H$, as depicted above. I'll consider $B$ the origin of a coordinate system, with the $x$ axis in the direction through $C$, the $y$ axis through $A$ and the $z$ axis through $G$. The extent of the box in the $x$ and $y$ direction are $32$, the extent in the $z$ direction is $64$.

Now I have a ball in plane $EAGB$, with the white dot marking its center. I want to obtain the coordinates of that ball. How can I derive this from the information in the image?

I know how to give 3d coordinates for all the corner points, and I also know that the plane $EAGB$ is described by the equation $x=0$. Therefore the ball must have that same $x$ coordinate, and I have to find its $y$ and $z$ coordinates.

I also have the coordinates of the center on the white ball, projected onto the plane $ABCD$. These are $x=1.7, y=15$. I want the 2d vector of the white ball on plane $EAGB$.

MvG
  • 42,596
Flier
  • 5
  • It is very hard to understand your question. Can you please include the image into the post? I guess that this answer of mine may help you, since it allows you to undo a projective transformation, i.e. transform from your picture to a situation where $EAGB$ form a rectangle of the dimensions you specified. – MvG Oct 23 '14 at 08:18
  • I took the liberty of completely rewriting your question. This is how I'd have written it: start with the picture of the situation you're referring to, then lay out all the relevant facts. In particular, be very clear about your definition of the coordinate system. Then state the question, and after that, show what you know and other things you assume might be useful. Note that I canceled a lot of cruft from the equation of the $EAGB$ plane. Make sure you understand that step, otherwise ask about that separately. Feel free to roll back if you don't agree this is your question. – MvG Oct 23 '14 at 08:45
  • Also note that I removed the portion about the pixel measurements from the image. Since I edited your picture (making it black on white to easier integrate with the page, and also cropping it to fit the page width), these coordinates would no longer apply. But I guess you'll want the description of how to compute this in general. One piece of information might be relevant: is the axis of your camera aligned along the $z$ direction, so that the rectangles $ABCD$ and $EFGH$ will always be exact rectangles in the picture? Or may you view the box at an angle occasionally? – MvG Oct 23 '14 at 08:49

1 Answers1

0

I used Cinderella to apply a projective transformation which maps $B$ to $B'=(0,0)$, $G$ to $G'=(64,0)$, $A$ to $A'=(0,32)$ and $E$ to $E'=(64,32)$. That map applied to $P$, the midpoint of your ball, is a point approximately at $P'\approx(31.58,13.95)$ so the coordinates of $P$ in 3d should be approximately $(0,13.95,31.58)$. From the picture you can see that there is a high uncertainty in the $z$ direction, due to the low resolution of the image and the large size of the white dot marker.

Screenshot

If you want to replicate this without using Cinderella, but doing the math yourself instead, then you'd have to compute a projective transformation given four points and their images.

Community
  • 1
MvG
  • 42,596
  • Thanks a ton for that. I have been busy recently and not able to check back for a while. I find it absurd that I need someone else to come in and edit a post for me to put an image in though. I had no idea how to word the question but it is what I needed. The cube may be looked at at an angle though. What steps would I do to find the coordinates on both planes EAGB and ABCD? – Flier Oct 29 '14 at 00:25
  • Also, what does the Lambda, Mu and Tau stand for in the linked post? What value do they have? – Flier Oct 29 '14 at 00:37
  • @Flier: You should be able to include images yourself. If you might look at the box at an angle, then the above approach is definitely the most suitable one, since it doesn't make any assumptions to the contrary. To find the position of a different ball which appears at the same position in the 2D image but is located on plane $ABCD$, you could do the same with those corners as reference points. $\lambda,\mu,\tau$ in that other post correspond to the last row of the projection matrix. You find them by solving a linear system of equations. – MvG Oct 29 '14 at 09:23