7

Prove that it is not possible to divide a disc into $7$ parts of equal area by means of three straight lines.

Background: I saw this question asked in a way which seemed to imply the possibility of a simple solution. The hint was given: what is the area on each side of a line? Well, obviously, $\frac37$ and $\frac47$ of the whole area, but I can't see where that gets me. Am I missing something really simple?

I tried doing some trig but it's a pain. Even "obvious" things seem difficult to prove rigorously, for example, that the lines intersect each other at $60^\circ$ angles.

Note that the division is possible if the disc is replaced by a (suitable) different shape. Therefore we must actually use the fact that the shape is a disc. (Or perhaps just the fact that it is convex?)

Any ideas? No lengthy trigonometric solutions please, I'm sure I could do that myself if I could be bothered to spend more time on it.

Please note that I am not asking for a ruler and compass construction, so this question and answer is not relevant.

Community
  • 1
David
  • 82,662
  • 1
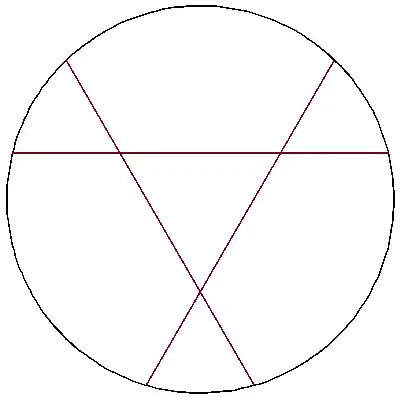
    I think you may simplify this to it is not possible to divide a disc into 7 parts remove equal area! – chouaib Oct 20 '14 at 00:12
  • 1
    @chouaib It is in fact easy to see you can divide a disc into 7 parts. – Euler....IS_ALIVE Oct 20 '14 at 00:24
  • @Euler....IS_ALIVE go ahead, show me (by a simple drawing) only – chouaib Oct 20 '14 at 00:26
  • @chouaib: draw a triangle inside a disc so that none of its vertices lie on the circle. Then extend the lines. – Clayton Oct 20 '14 at 00:27
  • @Clayton, GREAT!! that's the only way I could divide the disc into 7 parts me too. Now my question: isnt't it better to start proving from this point? take any two regions and prove they're not equal is a lot easier way to tackle this problem, right ? – chouaib Oct 20 '14 at 00:30
  • Appears convexity suffices; this could lead to an easier proof. – Will Jagy Oct 20 '14 at 00:32
  • 1
    Meanwhile, the 3/7 business cuts down the configuration space to, in effect, dimension two. Each line is a fixed distance from the origin. Fix one. The other two are given entirely by two relative angles. – Will Jagy Oct 20 '14 at 00:37

1 Answers1

2

Each line splits the disk into parts of areas $3/7 A$ and $4/7 A$, where $A$ is the area of the disk, and that determines the distance $d$ from the centre of the disk to the line. The general arrangement has to be something like

enter image description here

where the intersection of two lines is in the $4/7 A$ region for the other line. In order for the three wedge-shaped regions to have the same areas, the angles between each pair of lines has to be the same (so $\pi/3$). That should be enough information to determine the area of the central triangle, say. If it's not $1/7 A$, you're done.

Robert Israel
  • 448,999
  • Yes. For circle of radius 1, the distance of each line from the origin is $\delta \approx 0.112437096,$ the minimum area of the inner triangle is $\delta \sqrt{27} \approx 0.584240288,$ but $\pi/7 \approx 0.448798951.$ Th possible areas for the inner triangle are $\delta (\tan \alpha + \tan \beta + \tan \gamma )$ constrained by $\alpha + \beta + \gamma = \pi.$ Going to double check minimum vs. maximum for inner triangle. – Will Jagy Oct 20 '14 at 01:47