Sum of cubes proof

Question

Prove that for any natural number n the following equality holds:

$$ (1+2+ \ldots + n)^2 = 1^3 + 2^3 + \ldots + n^3 $$

I think it has something to do with induction?

Answer 1

By induction:

for $n=1$ it works. Then, suppose it works for a $n$. Then, $$(1+...+n+(n+1))^2=\underbrace{(1+...+n)^2}_{=1^3+...+n^3\ by\ hyp.}+2(1+...+n)(n+1)+(n+1)^2$$$$=1^3+...+n^3+(n+1)\big(2\underbrace{(1+...+n)}_{=\frac{n(n+1)}{2}}+(n+1)\big)$$$$=1^3+...+n^3+(n+1)\big(n(n+1)+(n+1)\big)$$$$=1^3+...+n^3+(n+1)(n+1)(n+1)$$$$=1^3+...+n^3+(n+1)^3.$$

Q.E.D.

Answer 2

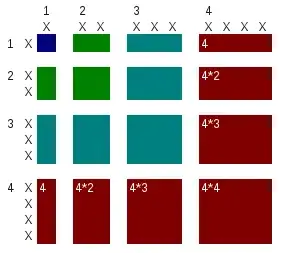
Here an illustration. The surface is the square of the sum. Prove that each added layer (in different color) is a the wanted cube and you will be done.

Answer 3

This solution assumes you are allowed to use $$ V_1 = \sum_{k=1}^{n} k = \frac{n(n+1)}{2}\\ V_2 = \sum_{k=1}^{n}k^2 = \frac{n(n+1)(2n+1)}{6} $$ Use the perturbation method (set the sum of cubes equal to $V_3$. Consider $$ S_n = \sum_{k=1}^{n}k^4 $$ then $$ S_n + (n+1)^4 = 1 + \sum_{k=1}^{n}(k+1)^4 = 1+S_n + 4 \sum_{k=1}^{n} k^3 + 4 \sum_{k=1}^{n} k^2 + \sum_{k=1}^{n} k +n $$ Obviously $S_n$ cancels out, you know $V_1$ and $V_2$, so you can get the value for $V_3$ and see that it's equal to $\frac{(n(n+1))^2}{4}$.

Answer 4

There is another way, if you like telescoping:

Let $V_k = (k-1)*k*(k+1)*(k+2)$ and $U_k$ = Vk+1 - Vk

$U_k$ = $k*(k+1)*(k+2)*[(k+3) - (k-1)]$ = $4*k*(k+1)*(k+2)$

= $4*k^3 + 12*k^2 + 8*k$

So if you know $1+4+9+..+n^2$ you can get your sum pretty easily by summing the $U_k$ from 1 to n-1, you will get:

$V_n$ -0 = $4*S_n + 12*C_n + 8*D_n$ , where $S_n$ is the partial sum of square and $C_n$ the partial sum of the cubes, and $D_n$ the partial sum of integers

$S_n = \frac{n*(n+1)*(2*n+1)}{6}$ , $D_n = \frac{n*(n+1)}{2}$, if you don't know their value