0

From Hungerford's "Algebra":

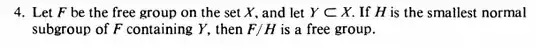
enter image description here

What type of tools does one have to tackle a problem like this? I seem at a loss at how to show a group is free at all. One can consider each group as the homomorphic image of a free group, but how does one work in the other direction?

user26857
  • 52,094
asd
  • 873
  • 1
    I would use universal properties. That is, for any group $G$ and function $f:X\setminus Y \to G$, I would show that $f$ extends to a unique homomorphism $F \to G$ whose kernel contains $Y$, hence $H$. – Andrew Dudzik Oct 13 '14 at 00:11

2 Answers2

2

The group $F/H$ is (isomorphic to) the free group on $X \setminus Y$, since it has the correct universal property: If $G$ is a group with underlying set $|G|$, then there are natural bijections $$\hom(F/H,G) \cong \{\phi \in \hom(F,G) : H \subseteq \ker(\phi)\}$$ $$= \{\phi \in \hom(F,G) : Y \subseteq \ker(\phi)\} \cong \{f \in \hom(X,|G|) : f|_Y = 1_G\}$$ $$ \cong \hom(X \setminus Y,|G|).$$

Martin Brandenburg
  • 163,620
-1

Take any function $X \setminus Y \to G$ where $G$ Is an arbitrary group. Then extend it is any way you want to a function $X \to G$. This induces a unique group homomorphism $F \to G$ which in turn induces a group homomorphism $F/H \to G$. A bit of work shows that this extension from $X \setminus Y$ to $F/H$ is unique, so the universal property of the free group is satisfied. So $F/H$ is free on $X \setminus Y$.

This all makes sense since we $X \setminus Y$ is (morally speaking) its own image in $F/H$.

nigel
  • 3,214
  • This is not correct. $X \to G$ has to send $Y$ to $1_G$, only then we get an extension to $F/H \to G$. Also, this "bit of work" uses universal properties anyway. – Martin Brandenburg Oct 13 '14 at 00:44