1

I'm interested in the growth of $$f(n):=\sum_{x=1}^{n-1} \left\lceil n-\sqrt{n^{2}-x^{2} } \right\rceil \quad \text{for}\quad n\rightarrow\infty $$

Progress

(From comments) I've got $$\frac{f(n)}{n^2} \ge 1-n^{-1} (1+\sum\limits_{x=1}^{n-1} \sqrt{1-\frac{x^2}{n^2}} )$$ and $$\frac{f(n)}{n^2}\le 1-n^{-1} (\sum\limits_{x=1}^{n-1} \sqrt{1-\frac{x^2}{n^2}} ) -1/n^2$$ as lower and upper bounds. Therefore, $$f(n)/n^2 \to C = 1- \int_{z=0}^1 \sqrt{1-z^2} \, dz. $$

Is there any way to improve this result? I mean to get an error term for $f(n)-Cn^2$?

Antonio Vargas
  • 24,993
user183847
  • 21

2 Answers2

2

Hints:

Establish that $$f(n) = \sum_{x=1}^{n-1} \left\lceil n - \sqrt{n^2 - x^2} \right\rceil \sim Cn^2$$ for some suitable constant $C$, by considering $$g(n) = \frac{f(n)}{n^2}.$$

Approximate $f$ for large $n$ with a suitable continuous summand, and regard the limiting behavior of $g$ as $n \to \infty$ as a Riemann integral.

heropup
  • 135,869
  • Ok I've dont like you said! So now I've got $1-n^{-1} (1+\sum\limits_{x=1}^{n-1} \sqrt{1-\frac{x^2}{n^2}} )$ as lower bound and $1-n^{-1} (\sum\limits_{x=1}^{n-1} \sqrt{1-\frac{x^2}{n^2}} ) -1/n^2$ as upper, which clearly converges. How do I get C=(1-PI/4)? – user183847 Oct 12 '14 at 20:22
  • Justify that we can write $$\frac{f(n)}{n^2} \approx \frac{1}{n} \sum_{x=1}^{n-1} \left( 1 - \sqrt{1 - (x/n)^2} \right)$$ hence $$\lim_{n \to \infty} g(n) = \int_{z=0}^1 1 - \sqrt{1-z^2} , dz.$$ – heropup Oct 12 '14 at 20:37
  • Thank you! Is there anyway to improve this result? I mean to get an error term for f(n)-Cn^2? So is there some way to get better bounds then the trivial ones I made? The ceiling function hurts! – user183847 Oct 12 '14 at 21:05
2

We can write

$$ \frac{f(n)}{n^2} = \frac{\delta_n}{n} + \frac{1}{n} \sum_{k=0}^{n-1} \left(1-\sqrt{1-k^2/n^2}\right), $$

where $0 \leq \delta_n \leq 1$. When $n$ is not the hypotenuse of a pythagorean triple we have the formula

$$ \delta_n = 1 - \frac{1}{n} - \frac{1}{n} \sum_{k=0}^{n-1} \left\{n - \sqrt{n^2-k^2}\right\}, \tag{$*$} $$

with $\{x\}$ denoting the fractional part of $x$.

It can be deduced from this answer of mine that

$$ \frac{1}{n} \sum_{k=0}^{n-1} \left(1-\sqrt{1-k^2/n^2}\right) = \int_0^1 \left(1-\sqrt{1-x^2}\right)dx - \frac{1}{2n} + O\left(n^{-3/2}\right), $$

so at least we know that

$$ \frac{f(n)}{n^2} = 1 - \frac{\pi}{4} + \frac{2\delta_n - 1}{2n} + O\left(n^{-3/2}\right). $$

The behavior of $\delta_n$ is harder to get a handle on. Numerically it seems to tend to $1/2$ as $n \to \infty$, as can be seen from the following plot.

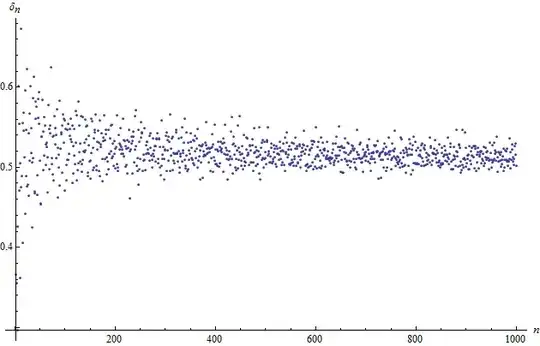
enter image description here

Because of this I would suspect that

$$ \frac{f(n)}{n^2} = 1 - \frac{\pi}{4} + o(n^{-1}) $$

as $n \to \infty$. Unfortunately without more information about $\delta_n$ this can't be made more precise.

The behavior $\delta_n \to 1/2$ is what we would expect if the summands $\left\{n - \sqrt{n^2-k^2}\right\}$ from $(*)$ were roughly uniformly distributed over the interval $[0,1]$. Perhaps this is the case in some specific sense, and I would be interested if someone could say something about it.

Community
  • 1
Antonio Vargas
  • 24,993