16

it's my first post here, so I apologize if I broke a rule!

I'm reading Introduction to Machine Learning and got stuck on VC dimension. Here's a quote from the book:

"...we see that an axis-aligned rectangle can shatter four points in two dimensions. Then VC(H), when H is the hypothesis class of axis-aligned rectangles in two dimensions, is four. In calculating the VC dimension, it is enough that we find four points that can be shattered; it is not necessary that we be able to shatter any four points..."

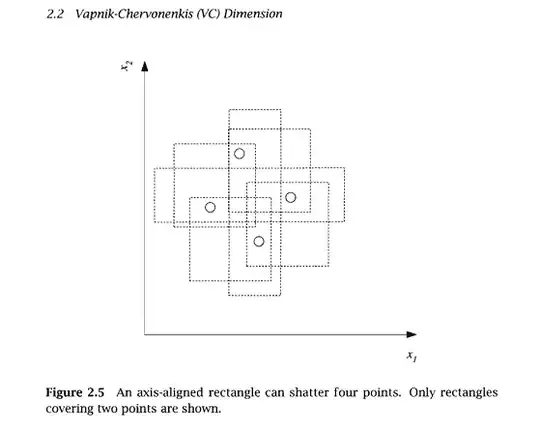
enter image description here

And I don't understand that. If it's enough to find some separable combinations, why can't we just choose a "rectangle with positive examples" from the image above, put another $n$ positive ones therein, and then say $VC(H)$ increased by $n$? And if all cases must be separable then why we don't consider 4 points placed on a line - which is in general not possible to shatter by a rectangle?

The same with the linear classifier example on wikipedia VC article - on their image four points are impossible to shatter, but we can come up with a layout where it is possible. And conversely, we can put 3 points (as "+", "-", "+") on a line and it won't be possible to separate the positives from the negatives by a linear classifier.

Can anyone explain where's my mistake?

andreister
  • 325
  • 16
    VC dimension works like this: You choose the points, then the adversary chooses the labeling. Finally you should be able to produce a hypothesis that correctly classifies that labeling of those points. If you are able to succeed for all labelings of the adversary, we say that the VC dimension is at least the number of points you were able to choose. – Srivatsan Jan 05 '12 at 14:23
  • @Srivatsan, your comment should definitely be posted as an answer :) – Serhiy Dec 31 '14 at 10:18

4 Answers4

10

I think you just need to think carefully about how your examples relate to the definition. The VC dimension of H is the maximum h such that there exists a set of cardinality h shattered by H. To show that VC(H)=4 you must show:

  • There is a set of cardinality 4 shattered by H, and
  • Any set of cardinality greater than 4 is not shattered by H

In the picture, they are doing the first thing - giving a lower bound on the VC dimension by giving an example of a set that is shattered. To show VC(H)<5 they should also show that no set of five points is shattered.

There will in general be lots of sets of various sizes that are not shattered, but that doesn't matter, essentially because VC dimension is a maximum over sets that are shattered. Your example of $n$ points on a line does not imply anything about the VC dimension. I hope this helps.

Colin McQuillan
  • 6,717
  • 1
    So finding a 3 point layout which is not possible to shatter with a line, or finding a 100 point layout which is possible to shatter with a rectangle - they're exceptional cases and don't matter because we consider "all possible" sets for a given N and identify how many of those sets are shattered - is that correct? Also, see Srivatsan's comment with "You choose the points, then the adversary chooses the labeling" - I find it very appealing, seems to solve my problem as well as your explanation. – andreister Jan 05 '12 at 14:43
  • 1
    Yes that's correct in the sense that for each size, either there are no sets shattered or there is at least one set shattered. For VC dimension you want to find the highest size with at least one set shattered. – Colin McQuillan Jan 05 '12 at 14:59
  • Hmmm. This "you want to find the highest size with at least one set shattered" is exactly what confused me in the first place. A rectangle hypothesis can shatter 5000 "specially placed" points but somehow we ignore this and say VC(H)=4. Why? Srivatsan's "You choose the points and the adversary selects the labels" rule sounds spot on, because then I won't be able to shatter "much". You seem to be explaining it more rigorously but so far it's been close to what they say in the book, and I feel like I'm not satisfied with their answer... – andreister Jan 05 '12 at 15:25
  • 1
    It is not correct that 'A rectangle hypothesis can shatter 5000 "specially placed" points'. The set of axis-aligned rectangles does not shatter any set of order five or more. – Colin McQuillan Jan 05 '12 at 17:03
  • Well, if VC dimension is about finding the size with at least one set shattered, then imagine 2500 "+" examples located inside a rectangle and 2500 "-" ones located outside. I don't see why we cannot do that, how exactly VC theory prevents us from choosing that one? – andreister Jan 09 '12 at 19:58
  • @andreister: a set can only be called shattered if every such assignment of "+"/"-" is covered by some member of the class (i.e. "for every subset there is..." etc - see the definition). The example of lines with lots of points is a set that is not shattered: there are subsets that cannot be covered. – Colin McQuillan Jan 09 '12 at 20:36
  • thanks for helping out. I'd try to summarize: [1] if I want to prove VC(H)=n, I may choose any layout for n points but then must prove that all "+/-" combinations can be separated with my classifier (and if that's true for all of them, we say that my set of n points is shattered by the classifier), and also [2] it's enough to find just one such layout of n points to prove VC(H)=n. Does that sound correct? Thanks! – andreister Jan 10 '12 at 08:26
  • Pretty much, except that just shows that VC(H) is at least n. – Colin McQuillan Jan 10 '12 at 08:45
  • Aha that makes sense - thanks! – andreister Jan 11 '12 at 08:41
0

@andreister, just adding some color:

The confusion arises because the definition of VC dimension involves BOTH an existential qualifier ("there exists"), and a universal qualifier ("for all"):

Note that, if the VC dimension is h, then there exists at least one set of h points that can be shattered, but it in general it will not be true that every set of h points can be shattered Burgess (1998)

Thus, one such set of points has to exist, but their shattering == for all labelings == a universal assertion.

vijucat
  • 119
0

The VC dimension of a hypothesis class, H is the cardinality of the largest set which can be shattered by a H .The requirement is you should be able to find at least one such set of points for which you can find a H that shatters (or you can always find a member of H that can classify every possible labelling of a ) particular set.

Now, consider the given set of 3 points (vertices of a triangle). You can find a h that correctly classifies every possible labelling of the set. It doesn't matter you can't do it for another set of 3 points (three points on a line). The sufficient condition is you find at least one such set.

Whereas, sure you could think of a labelling of 4 points (say the points have the same label) that a two dimensional classifier could properly classify, but can it properly classify every possible labelling of the the set of points? Think about it. You'll realise there exists no such pair.

Ayoosh Kathuria
  • 1
0

@Srivatsan's explanation makes sense to me. I had this same problem when I started learning this. You have to allow any possible point dichotomy, and then prove that you can shatter that. Hence, if you find one combination of classes for a number of points that you can't shatter, that machine must have a VC dimension smaller than that number of points. Hence, the fact that a linear classifier can't shatter XOR means that you can't handle anything larger than 3 points, which is an illustration of Burges' n(-dimension)+1 rule for linear classifier VC dimension.

bright-star
  • 1,161